Berechnung eines Rohrleitungssystems

Strömungswerte

Volumen- und Massenstrom

Q  = Volumenstrom (m³/s)
m   = Massenstrom (kg/s)
d _i = Rohrinnendurchmesser (m)
v   = Strömungsgeschwindigkeit (m/s)
ρ   = Dichte (kg/m³)

Q  = Volumenstrom (m³/s)
m   = Massenstrom (kg/s)
d _i = Rohrinnendurchmesser (m)
v   = Strömungsgeschwindigkeit (m/s)
ρ   = Dichte (kg/m³)

Druckverlust inkompressible Fluide (Flüssigkeiten)

Δp  = Druckverlust (Pa)
ρ   = Dichte (kg/m³)
v   = Strömungsgeschwindigkeit (m/s)
λ   = Rohrreibungszahl (-)
d _i = Rohrinnendurchmesser (m)
L _R = Rohrleitungslänge (m)
ζ   = Widerstandsbeiwert (-)
m   = Massenstrom (kg/s)
L _Äq = Äquivalente Rohrleitungslänge (m)

Δp  = Druckverlust (Pa)
ρ   = Dichte (kg/m³)
v   = Strömungsgeschwindigkeit (m/s)
λ   = Rohrreibungszahl (-)
d _i = Rohrinnendurchmesser (m)
L _R = Rohrleitungslänge (m)
ζ   = Widerstandsbeiwert (-)
m   = Massenstrom (kg/s)
L _Äq = Äquivalente Rohrleitungslänge (m)

Druckverlust kompressible Fluide (Gase und Dämpfe)

Δp  = Druckverlust (Pa)
p _A = Druck Rohranfang (Pa)
ρ _A = Dichte Rohranfang (kg/m³)
v   = Strömungsgeschwindigkeit Rohranfang (m/s)
λ   = Rohrreibungszahl (-)
L _R = Rohrleitungslänge (m)
d _i = Rohrinnendurchmesser (m)
ζ   = Widerstandsbeiwert (-)
T _m = mittlere Fluidtemperatur (K)
T _A = Fluidtemperatur Rohranfang (K)
T _E = Fluidtemperatur Rohrende (K)
m   = Massenstrom (kg/s)
L _Äq = Äquivalente Rohrleitungslänge (m)

Geodätischer Höhenunterschied

p_E = Druck Rohrende (Pa)
p _A = Druck Rohranfang (Pa)
Δp   = Druckverlust (Pa)
ρ _A = Dichte Rohranfang (kg/m³)
ρ _E = Dichte Rohrende (kg/m³)
v _A = Strömungsgeschwindigkeit Rohranfang (m/s)
v _E = Strömungsgeschwindigkeit Rohrende (m/s)
g   = Erdbeschleunigung (m/s²)
Δh   = Höhenunterschied (m)
h _A = Geodätische Höhe Rohranfang (m)
h _E = Geodätische Höhe Rohrende (m)
Δp _G = Geodätischer Höhenunterschied (Pa)

Weitere Formeln und Druckverlustwerte auf der Webseite

Weiterführende Berechnungen zu Druckverlustberechnungen von Rohrleitungen ist in dem Kapitel Strömungstechnik aufgeführt.
Zu folgenden Punkten sind die Formeln bzw. Berechnungsprogramme vorhanden:
- Druckverlustberechnung gerader Rohrleitungen inkompressibler Medien (Flüssigkeiten)
- Druckverlustberechnung gerader Rohrleitungen kompressibler Medien (Gase)
- Druckverlustberechnung von Komponenten mit dem Zetawert
- Zetawert Diagramme bzw. Tabellen

Berechnungsprogramme:
- Druckverlustberechnung gerade Rohrleitung inkompressibler Medien (Flüssigkeiten)
- Druckverlustberechnung gerade Rohrleitung kompressibler Medien (Gase)
- Druckverlustberechnung eines Rohrleitungsstrangs
- Kv Wertberechnung von Armaturen bei Flüssigkeiten
- Kv Wertberechnung von Armaturen bei gasförmigen Medien

Festigkeitswerte

Rohrspannungen

Tangential- und Axialspannungen in einem durch Innendruck belasteten Rohr, das an den Enden geschlossen ist.

σ_t = Tangentialspannung (N/mm²)
σ _a = Axialspannung (N/mm²)
p   = Innendruck (N/mm²) - 1 N/mm² = 10 bar
d _m = Mittlerer Rohrdurchmesser (mm)
s   = Rohrwandstärke (mm)

σ_t = Tangentialspannung (N/mm²)
σ _a = Axialspannung (N/mm²)
p   = Innendruck (N/mm²) - 1 N/mm² = 10 bar
d _m = Mittlerer Rohrdurchmesser (mm)
s   = Rohrwandstärke (mm)

Rohrwandstärke

Die Rohrwandstärke wird nach der Kesselformel berechnet.

s  = Rohrwandstärke (mm)
p   = Innendruck (N/mm²) - 1 N/mm² = 10 bar
d _m = Mittlerer Rohrdurchmesser (mm)
d _a = Rohraußendurchmesser (mm)
d _i = Rohrinnendurchmesser (mm)
σ _zul = zul. Spannung (N/mm²)

s  = Rohrwandstärke (mm)
p   = Innendruck (N/mm²) - 1 N/mm² = 10 bar
d _m = Mittlerer Rohrdurchmesser (mm)
d _a = Rohraußendurchmesser (mm)
d _i = Rohrinnendurchmesser (mm)
σ _zul = zul. Spannung (N/mm²)

Beuldruck - Unterdruck

In bestimmten Einsatzfällen sind Rohrleitungen einem äußeren Überdruck oder innerem Unterdruck ausgesetzt. Der kritische Beuldruck berechnet sich wie folgt:

p_kr = kritischer Beuldruck (N/mm²)
E   = E-Modul (N/mm²)
ν   = Querdehnungszahl (-)
s   = Wanddicke (mm)
r   = mittl. Rohrradius (mm)
r _a = Rohraußenradius (mm)
r _i = Rohrinnenradius (mm)
d _a = Rohraußendurchmesser (mm)
p _a,zul = zulässiger Beuldruck (N/mm²)
S   = Sicherheit (-) / elast. Spannungszustand S = 3

p_kr = kritischer Beuldruck (N/mm²)
E   = E-Modul (N/mm²)
ν   = Querdehnungszahl (-)
s   = Wanddicke (mm)
r   = mittl. Rohrradius (mm)
r _a = Rohraußenradius (mm)
r _i = Rohrinnenradius (mm)
d _a = Rohraußendurchmesser (mm)
p _a,zul = zulässiger Beuldruck (N/mm²)
S   = Sicherheit (-) / elast. Spannungszustand S = 3

Längenänderung durch den Innendruck

Die durch den inneren Überdruck hervorgerufene Längsdehnung einer geschlossenen und reibungfreien gelagerten Rohrstrecke beträgt:

ΔL_p = Längenänderung (mm)
p   = Innendruck (N/mm²) / 1 N/mm² = 10 bar
ν   = Querdehnungszahl (-)
E   = E-Modul (N/mm²)
L   = Rohleitungslänge (mm)
d _a = Rohraußendurchmesser (mm)
d _i = Rohrinnendurchmesser (mm)

ΔL_p = Längenänderung (mm)
p   = Innendruck (N/mm²) / 1 N/mm² = 10 bar
ν   = Querdehnungszahl (-)
E   = E-Modul (N/mm²)
L   = Rohleitungslänge (mm)
d _a = Rohraußendurchmesser (mm)
d _i = Rohrinnendurchmesser (mm)

Rohrdehnung durch Wärme

Wärmedehnung

Im Betrieb dehnt sich die Rohrleitung aus, gegenüber dem Ausgangszustand bei der Montage oder bei Stillstand der Rohrleitung. Maßgebend für die Rohrdehnung ist die Temperaturdifferenz und der Wärmeausdehnungskoeffizient der Werkstoffabhängig ist.

Δl  = Wärmedehnung (m)
L ₀ = Rohrleitungslänge (m)
β   = Ausdehnungskoeffizient (1/K)
Δt   = Temperaturdifferenz (K)

Δl  = Wärmedehnung (m)
L ₀ = Rohrleitungslänge (m)
β   = Ausdehnungskoeffizient (1/K)
Δt   = Temperaturdifferenz (K)

Anhaltswerte: Längendehnung von 1 m Rohr:
- Stahl bei Δt ≈ 100 K ca. 1,1 mm/m bei Δ t ≈ 400 K ca. 5,6 mm/m
- Edelstahl bei Δt ≈ 100 K ca. 1,6 mm/m bei Δt ≈ 500 K ca. 9,0 mm/m

Druck-Spannung im Rohr durch die Rohrdehnung

Bei einem beidseitig eingespannten Rohr, entstehen Druck-Spannungen im Rohr.

ε  = Dehnung (-)
Δl   = Wärmedehnung (m)
L ₀ = Rohrleitungslänge (m)
E   = Elastizitätsmodul (N/mm²)
σ _d = Druck-Spannung (N/mm²)
β   = Ausdehnungskoeffizient (1/K)
Δt   = Temperaturdifferenz (K)

ε  = Dehnung (-)
Δl   = Wärmedehnung (m)
L ₀ = Rohrleitungslänge (m)
E   = Elastizitätsmodul (N/mm²)
σ _d = Druck-Spannung (N/mm²)
β   = Ausdehnungskoeffizient (1/K)
Δt   = Temperaturdifferenz (K)

Zul. Temperaturdifferenz bei Erreichen der zul. Spannung

σ_zul = Zulässige Spannung (N/mm²)
R _p,0.2 = Streckgrenze (N/mm²)
S   = Sicherheit (-)
Δt   = Temperaturdifferenz (K)
E   = Elastizitätsmodul (N/mm²)
β   = Ausdehnungskoeffizient (1/K)

σ_zul = Zulässige Spannung (N/mm²)
R _p,0.2 = Streckgrenze (N/mm²)
S   = Sicherheit (-)
Δt   = Temperaturdifferenz (K)
E   = Elastizitätsmodul (N/mm²)
β   = Ausdehnungskoeffizient (1/K)

Beispiel: Für S235JR (St37) mit einem R_p,0.2 = 235 N/mm², E-Modul = 210000 N/mm², Sicherheit S = 1,5 und einem Ausdehnungskoeffizienten β = 11*10^-6 1/K beträgt die zulässige Temperaturdifferenz 68 K.

Axialkräfte an den Einspannstellen durch die Wärmedehnung

Bei einem beidseitig eingespannten Rohr tritt folgende Axialkraft an den Einspannstellen auf, wenn die zulässige Axialspannung erreicht ist.

F  = Axialkraft (N)
σ _zul = Zulässige Spannung (N/mm²)
A   = Querschnitt der Rohrwandung (mm²)

F  = Axialkraft (N)
σ _zul = Zulässige Spannung (N/mm²)
A   = Querschnitt der Rohrwandung (mm²)

Knicklänge bei Erreichen der elastischen Knickspannung

Auf Grund Ihrer schlanken Form sind Rohre auch knickgefährdet. Bei überschreiten der elastischen Knickspannung (Grenzschlankheitsgrad nach Euler), kann es zum Versagen der Rohrleitung führen.

Grenzschlankheitsgrad nach Euler

Knicklänge bei gelenkiger Lagerung - Eulerfall 2

Knicklänge bei fest eingespannter Lagerung
Eulerfall 4

σ_k,p = Knickspannung bei Grenzschlankheitsgrad (N/mm²)
E   = E-Modul (N/mm²)
λ _p = Grenzschlankheitsgrad (-)
σ _d,zul = Zul. Druckspannung (N/mm²)
L _k = Knicklänge (mm)
I   = Flächenträgheitsmoment (mm⁴)
A   = Rohrquerschnitt (mm²)
σ _zul = Zul. Knickspannung (N/mm²)
d _a = Rohraußendurchmesser (mm)
d _i = Rohrinnendurchmesser (mm)

σ_k,p = Knickspannung bei Grenzschlankheitsgrad (N/mm²)
E   = E-Modul (N/mm²)
λ _p = Grenzschlankheitsgrad (-)
σ _d,zul = Zul. Druckspannung (N/mm²)
L _k = Knicklänge (mm)
I   = Flächenträgheitsmoment (mm⁴)
A   = Rohrquerschnitt (mm²)
σ _zul = Zul. Knickspannung (N/mm²)
d _a = Rohraußendurchmesser (mm)
d _i = Rohrinnendurchmesser (mm)

Das erste Diagramm zeigt den Verlauf des Grenzschlankheitsgrads in Abhängigkeit der Knickspannung.
Die Abhängigkeit der freien Knicklänge von der Knickspannung beim Grenzschlankheitsgrad von Stahlrohren, zeigt das zweite Diagramm.

Ausgleich von Rohrlängenveränderungen [1]

Durch eingebaute Dehnungskomponenten können die auftretenden Spannungen und Kräfte auf die Lagerelemente (Bauwerk) verringert werden.
Dehnungskomponenten:
- Biegeschenkel - L- oder Z-Bögen
- U-Bögen
- Lyra-Bögen (Omega-Bögen)
- Kompensatoren

Bei Biegeschenkel ist die Biegespannung an der Einspannstelle für die Ausladelänge L_A maßgebend. Auf Grund der Belastung durch den Innendruck, ist für die zulässige Biegespannung des Biegeschenkels nur noch eine geringere Spannung anzusetzen.

L-Bogen

Wärmedehnungen können im Leitungsverlauf durch L-Bogen (Biegeschenkel) aufgenommen werden.

L_A,L = Biegeschenkellänge (mm)
E   = E-Modul (N/mm²)
Δl   = Wärmedehnung (mm)
d _a = Rohraußendurchmesser (mm)
C _L = Werkstoffkonstante (-)
σ _zul = zul. Spannung (N/mm²)
K   = Werkstoffkennwert (N/mm²)
ν _N = Ausnutzung der Berechnungsspannung (-) = 0,85
S   = Sicherheit (-) = 1,5
i  = Spannungserhöhungsfaktor (-)

L_A,L = Biegeschenkellänge (mm)
E   = E-Modul (N/mm²)
Δl   = Wärmedehnung (mm)
d _a = Rohraußendurchmesser (mm)
C _L = Werkstoffkonstante (-)
σ _zul = zul. Spannung (N/mm²)
K   = Werkstoffkennwert (N/mm²)
ν _N = Ausnutzung der Berechnungsspannung (-) = 0,85
S   = Sicherheit (-) = 1,5
i  = Spannungserhöhungsfaktor (-)

U-Bogen

Die Längenausdehnung beim U-Bogen wird auf zwei Rohre aufgeteilt, dadurch verringert sich die Ausladelänge.

L_A,U = Ausladelänge (mm)
C _U = Werkstoffkonstante (-)
Δl   = Wärmedehnung (mm)
d _a = Rohraußendurchmesser (mm)
E   = E-Modul (N/mm²)
σ _zul = zul. Spannung (N/mm²) - siehe oben

L_A,U = Ausladelänge (mm)
C _U = Werkstoffkonstante (-)
Δl   = Wärmedehnung (mm)
d _a = Rohraußendurchmesser (mm)
E   = E-Modul (N/mm²)
σ _zul = zul. Spannung (N/mm²)) - siehe oben

Vorspannung von L- bzw. U-Bogen

Wird der L- bzw. U-Bogen vorgespannt, so verringert sich die Dehnungsaufnahme bzw. die Auslandelänge wie folgt.

Δl  = Wärmedehnung mit Vorspannung (mm)
Δl ₀ = Wärmedehnung ohne Vorspannung (mm)
x   = Vorspannung (%)
L _A = Ausladelänge mit Vorspannung (mm)
L _A,0 = Ausladelänge ohne Vorspannung (mm)

Δl  = Wärmedehnung mit Vorspannung (mm)
Δl ₀ = Wärmedehnung ohne Vorspannung (mm)
x   = Vorspannung (%)
L _A = Ausladelänge mit Vorspannung (mm)
L _A,0 = Ausladelänge ohne Vorspannung (mm)

[1] Wagner: Rohrleitungstechnik

Wärme- und Temperaturverluste

Formeln und Berechnungsprogramme zu Wärme- und Temperaturverluste

Die Formel und Berechnungsprogramme für den Wärme und Temperaturverlust auf dieser Website, finden sie auf folgenden Seiten:

Stützweiten

Für einfache Rohrsysteme kann die Stützweitenberechnung nach folgenden Kriterien erfolgen:
Begrenzung der Spannung:
Bei voller Ausnutzung der Rohrspannung durch den Innendruck, wird eine zulässige Biegespannung von 40 N/mm² angesetzt. Wird die Rohrleitung durch den Innendruck nicht voll belastet, kann eine höhere Spannung angesetzt werden.
Begrenzung durch maximale Durchbiegung:
Als zulässige Durchbiegung werden folgende Werte angesetzt:
≤ DN 50 - f_zul = 3 mm
> DN 50 - f_zul = 5 mm
Zur Bestimmung der Stützweite werden die unten aufgeführten Biegeträgeranordnungen zugrunde gelegt.

Anhaltswerte des spez. Gewichts für die der Streckenlasten bei Rohrleitungen

Maßgebende Belastungen sind das Rohreigengewicht, Dämmung und das Rohrfüllgewicht. Zusätzlich könne noch Schnee- und Windlasten zu berücksichtigen sein.

Stützweite von Rohrleitungen bei Streckenlasten

Die Berechnung der Stützweite wird vereinfacht auf die beiden Fälle als Biegeträger mit gelenkiger oder fest eingespannter Lagerung berechnet.
Die Annahme einer fest eingespannten Lagerung trifft nur in wenigen Ausnahmefällen zu, z. B. Anschluss eines kurzen Rohrstückes an einen großen steifen Behälter. Die unten aufgeführten Formeln berücksichtigen nur die Streckenlasten, sind gegenüber der DINEN 13480 aber einfacher zu handhaben, da die Ergebnisse nicht iterativ berechnet werden müssen.

Stützweite bei gegebener Durchbiegung

Gelenkige Lagerung

Starre Lagerung

L  = Stützlänge (mm)
E   = E-Modul (N/mm²)
I   = Flächenträgheitsmoment (mm⁴)
f _max = zul. Durchbiegung (mm) - ≤ DN 50 = 3 mm / > DN 50 = 5 mm
q   = Streckenlast (N/mm)

L  = Stützlänge (mm)
E   = E-Modul (N/mm²)
I   = Flächenträgheitsmoment (mm⁴)
f _max = zul. Durchbiegung (mm) - ≤ DN 50 = 3 mm / > DN 50 = 5 mm
q   = Streckenlast (N/mm)

Stützweite bei gegebener zulässiger Biegespannung

Gelenkige Lagerung

Starre Lagerung

L  = Stützlänge (mm)
E   = E-Modul (N/mm²)
I   = Flächenträgheitsmoment (mm⁴)
σ _zul = zul. Biegespannung (N/mm²)
q   = Streckenlast (N/mm)

L  = Stützlänge (mm)
E   = E-Modul (N/mm²)
I   = Flächenträgheitsmoment (mm⁴)
σ _zul = zul. Biegespannung (N/mm²)
q   = Streckenlast (N/mm)

Stützweitenberechnung nach DIN EN 13480 Anhang Q - Streckenlast und Einzellast

Bei der Stützweitenberechnung nach DIN EN 13480 Anhang Q werden Streckenlasten und Einzellasten berücksichtigt, z. B. durch Armaturen.
Achtung: Bei gleichzeitiger Belastung durch Streckenlast und Einzellast, können die Gleichungen nicht nach der Stützweite aufgelöst werden, sondern diese müssen iterativ gelöst werden.

Träger auf zwei Stützen

Kragträger

Durchlaufträger - Einzellast in allen Feldern

Durchlaufträger - F* Einzellast nur im jeweiligen Feld F/q ≤ 0,38 * L^*

Durchlaufträger - F* Einzellast nur im jeweiligen Feld F/q > 0,38 * L^*

L_n,i = Stützlänge, Kraglänge (mm)
f   = zul. Durchbiegung (mm)- ≤ DN 50 = 3 mm / > DN 50 = 5 mm
F   = Einzellast (N)
E   = E-Modul (N/mm²)
I   = Trägheitsmoment (mm⁴)
W   = Widerstandsmoment (mm³)
q   = Streckenlast (N/mm)
i   = Spannungserhöhungsfaktor (-)

Spannungserhöhungsfaktor i

	Formfaktor H	Spannungs- erhöhungsfaktor i (≥ 1)
gerades Rohr	1	1
Rohrbogen
Gepresstes Einschweiss-Reduzierstück		α in Grad
T-Stück mit auf- bzw. eingeschweißtem oder ausgehalstem Stutzen
Gepresstes Einschweiss T-Stück
Widerstandsmoment Stutzen	s x als kleinerer Wert von sx1 = s und sx2 = i*sA

Rohrleitungsabstand

Mindestabstand zum Bauwerk und benachbarten Rohrleitungen

Zur Montage der Rohrleitungen und Dämmung sowie zu Instandhaltungszwecken ist nach DIN 4140 zwischen Außenkontur der Rohrleitung und
- benachbarten Rohrleitungen
- Ausrüstungen und Aggregaten
- Baukörper (Decken, Wände, Träger)
ein Zwischenraum von mindestens 100 mm erforderlich.

Rohrleitungsabstand bei angeflanschten Rohrleitungen

Zur Minimierung der Abstände bei angeflanschten Rohrleitungen, sind die Flanschverbindungen versetzt anzuordnen.
Abstand s = Isolierdicke
Abstand x = Schraubenlänge + 30 mm
Abstand a = > 100 mm

Achsabstand der Rohrleitungen an Absperrklappen

Schallpegelberechnung von Armaturen für Gase und Flüssigkeiten

Die unten aufgeführten Formel zur Berechnung der Schalldruckpegel beziehen sich auf industrielle Rohrleitungen.

Schallpegelberechnung von Armaturen für Gase und Dämpfe

Die Berechnung des Schalldruckpegels von Armaturen erfolgt nach VDMA 24422.

Gesamtschallpegel

Schalldruckpegelanteil, abhängig vom Durchfluss-Koeffizienten k_vs und dem Eintrittsdruck P₁.

Schalldruckpegelanteil, abhängig vom Druckverhältnis zwischen Ein- und Austritt, bezogen auf ein kritisches Druckverhältnis P2 / P1 = 0,546.

Schalldruckpegelanteil, abhängig von der Eintrittstemperatur T1 und der Normdichte ρ_N.

Armaturenspezifischer Schalldruckpegelanteil

Je nach Bauart ist der charakteristische Schalldruckpegelanteil aus den Herstellerunterlagen zu entnehmen. Ist im Planungsstadium der Armaturentyp noch nicht bekannt, kann mit dem im Diagramm dargestellten Wert gerechnet werden.

Schalldämmung der Armaturenwandung

Bei der Berechnung des Schalldruckpegels ist bereits eine Bezugswanddicke berücksichtigt. Weicht die tatsächliche Anschlusswanddicke von e₄₀ ab, ist der Korrekturfaktor R_R erforderlich.

Nennweite DN	≤40	50	80	100	150	200	250	300	400	500
Bezugswanddicke e40 (mm)	2,6	2,9	3,2	3,6	4,5	6,3	7,1	8	11	14,2

Zulässige Austrittsgeschwindigkeit

Die Formel für den Gesamtschallpegel setzt voraus, dass die Austrittsgeschwindigkeit Ma ≤ 0,3 eingehalten wird.

L_A = Gesamtschalldruckpegel (dB)
ΔL _A1G = Schalldruckpegelanteil des Durchfluss-Koeffizienten k_vs und dem Eintrittsdruck P1
ΔL _A2G = Schalldruckpegelanteil des Druckverhältnis P1 zu P2
ΔL _A3G = Schalldruckpegelanteil der Eintrittstemperatur und Normdichte
ΔL _G = Armaturenspezifischer Schalldruckpegelanteil
ΔR _R = Schalldämmung der Armaturenwandung
k _vs = Durchflusskoeffizient (m³/h)
P ₁ = Eintrittsdruck (bar)
P ₂ = Austrittsdruck (bar)
T ₁ = Eintrittstemperatur (K)
ρ _N = Normdichte (kg/m³)
e ₄₀ = Bezugswanddicke (mm)
e _S = Anschlusswanddicke (mm)
a ₂ = Austrittsgeschwindigkeit (m/s)
a _F = Schallgeschwindigkeit (m/s)

Schallpegelberechnung von Armaturen für Flüssigkeiten

Die Berechnung des Schalldruckpegels von Armaturen erfolgt nach VDMA 24422.

Gesamtschallpegel

Schalldruckpegelanteil, abhängig vom Durchfluss-Koeffizienten k_vs und der Druckdifferenz P₁ - P_v.

Kavitationsabhängiger Schalldruckpegelanteil

Mit der armaturenspezifischen Kenngröße z_v (akustischer Beiwert) kann bestimmt werden, ob kavitationsfreie oder -behaftete Strömung vorliegt, in Abhängigkeit Auslastungsgrad der Armatur. Einige typische Kennlinien sind in dem folgenden Diagramm dargestellt, bzw. sollten in den Herstellerunterlagen enthalten sein.

Kavitationsfreie Strömung

Kavitationsbehaftete Strömung

Schalldruckpegelanteil, abhängig von der Dichte ρ_G.

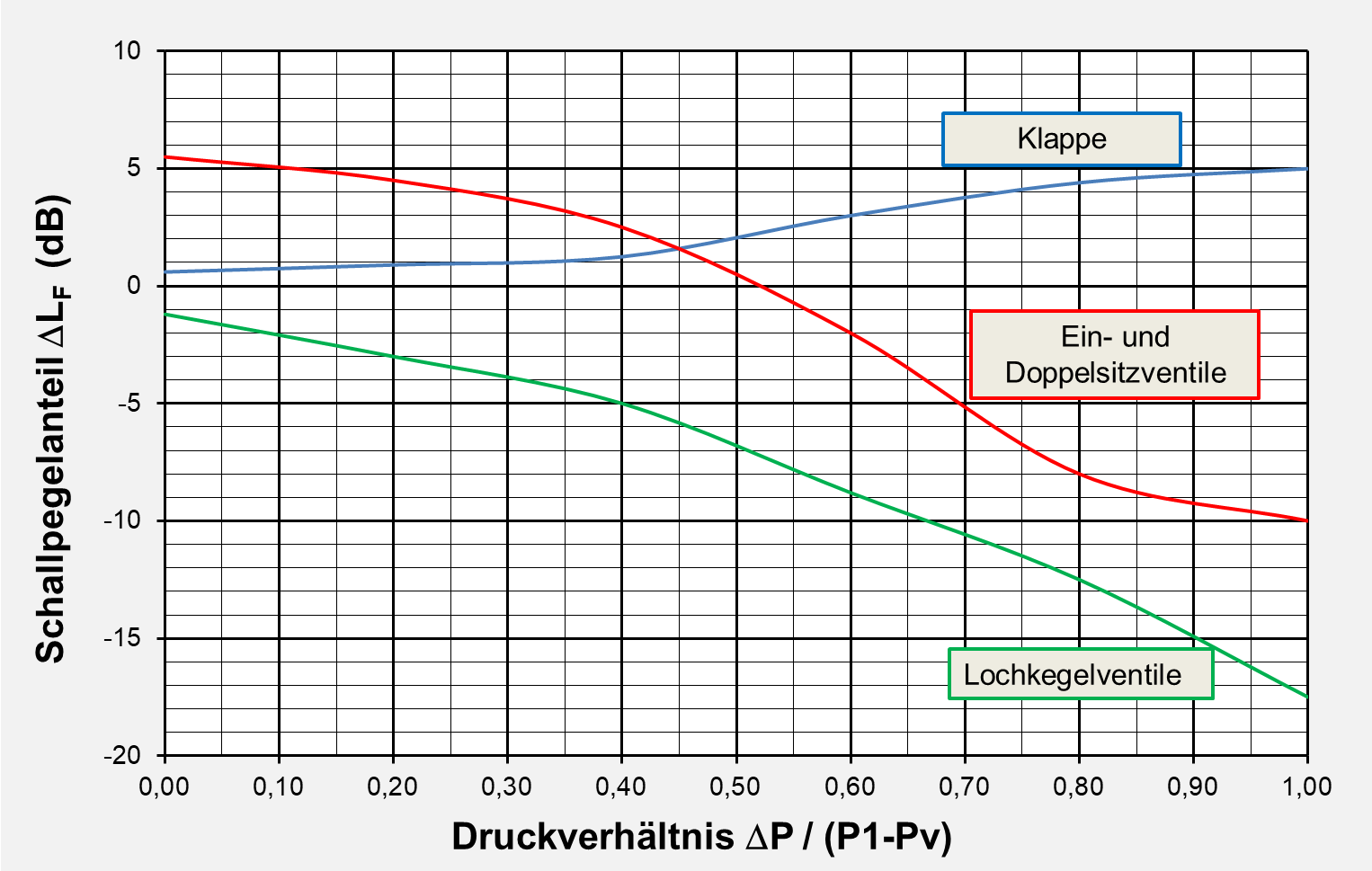
Armaturenspezifischer Schalldruckpegelanteil

Je nach Bauart ist der charakteristische Schalldruckpegelanteil aus den Herstellerunterlagen zu entnehmen. Ist im Planungsstadium der Armaturentyp noch nicht bekannt, kann mit dem im Diagramm dargestellten Wert gerechnet werden.

Schalldämmung der Armaturenwandung

Bei der Berechnung des Schalldruckpegels ist bereits eine Bezugswanddicke berücksichtigt. Weicht die tatsächliche Anschlusswanddicke von e₄₀ ab, ist der Korrekturfaktor R_R erforderlich.

Nennweite DN	≤40	50	80	100	150	200	250	300	400	500
Bezugswanddicke e40 (mm)	2,6	2,9	3,2	3,6	4,5	6,3	7,1	8	11	14,2

Zulässige Austrittsgeschwindigkeit

Die Formeln für den Gesamtschallpegel gelten für eine Austrittsgeschwindigkeit von:

L_A = Gesamtschalldruckpegel (dB)
ΔL _A1F = Schalldruckpegelanteil des Durchfluss-Koeffizienten k_vs und der Druckdifferenz P₁-P_v
ΔL _A2F = Kavitationsabhängiger Schalldruckpegelanteil
ΔL _A3F = Schalldruckpegelanteil abhängig von der Dichte
ΔL _F = Armaturenspezifischer Schalldruckpegelanteil
ΔR _R = Schalldämmung der Armaturenwandung
k _vs = Durchflusskoeffizient 100% Öffnung (m³/h)
k _v = Durchflusskoeffizient bei anteiliger Öffnung (m³/h)
Y _v = Auslastungsgrad (-)
z _v = akustischer Beiwert (-)
X _F = Druckverhältnis (-)
P ₁ = Eintrittsdruck (bar)
P ₂ = Austrittsdruck (bar)
P _v = Siededruck der Flüssigkeit (bar)
ΔP   = Druckdifferenz P1-P2 (bar)
ρ _kw = Dichte von Kaltwasser bei Raumtemperatur (kg/m³)
ρ ₀ = Dichte bei Betriebsbedingungen (kg/m³)
e ₄₀ = Bezugswanddicke (mm)
e _S = Anschlusswanddicke (mm)
a ₂ = Austrittsgeschwindigkeit (m/s)

Strömungsrauschen in der Rohrleitung bei Gasen

Das Strömungsrauschen in der Rohrleitung wird hauptsächlich durch die Strömungsgeschwindigkeit des Fluides bestimmt. Nach VDI 3733 kann der Schallleistungspegel in der Rohrleitung bei einer Strömungsgeschwindigkeit < 0,3 Ma wie folgt berechnet werden.

L_Ri = Schallleistungspegel (dB(A))
w _R = Strömungsgeschwindigkeit (m/s)
P ₀ = Betriebsdruck (bar)
d _i = Rohrinnendurchmesser (mm)
R   = Gaskonstante (J/(kg*K))
T ₀ = Betriebstemperatur (K)
κ   = Adiabaten Exponent (-)