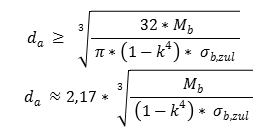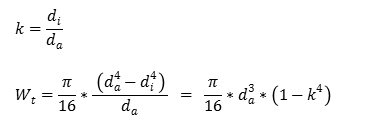Berechnung von Wellen und Achsen
Wellendurchmesser
Wellendurchmesser bei Biegebelastung
Allgemeine Biegespannungs-Formel

Wellen-AuĂendurchmesser einer Vollwelle bei Biegung

Wellen-AuĂendurchmesser einer Hohlwelle bei Biegung
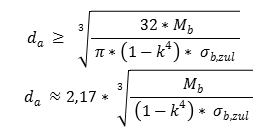
Widerstandsmoment einer Hohlachse bei Biegung

Wellen-Innendurchmesser einer Hohlachse bei Biegung


Ďb = Biegespannung (N/mm²)
M b = Biegemoment (Nmm)
W b = Widerstandsmoment bei Biegung (mmÂł)
d a = Wellen-AuĂendurchmesser (mm)
d i = Wellen-Innendurchmesser (mm)
Ď b,zul = zulässige Biegespannung (N/mm²)
k = Durchmesser-Verhältnis (-)
Ďb = Biegespannung (N/mm²)
M b = Biegemoment (Nmm)
W b = Widerstandsmoment bei Biegung (mmÂł)
d a = Wellen-AuĂendurchmesser (mm)
d i = Wellen-Innendurchmesser (mm)
Ď b,zul = zulässige Biegespannung (N/mm²)
k = Durchmesser-Verhältnis (-)
nach oben
nach oben
Wellen mit gleicher Festigkeit - Angeformte Wellen
GroĂe und schwere Wellen werden aus GewichtsgrĂźnden häufig als Träger mit gleicher Festigkeit ausgebildet.
Der oben ermittelte Durchmesser, bei Biegebelastung, ist nur an der Stelle mit dem hĂśchsten Biegemoment erforderlich.
An allen anderen Querschnittsstellen kann der Durchmesser entsprechend dem auftretenden Biegemomentes kleiner sein.
Somit ergibt sich ein RotationskĂśrper, der durch eine kubische Parabel begrenzt ist. Die Achse wird durch zylindrische oder kegelige Abstufungen ausgebildet.
Wellendurchmesser bei gegebenem Biegemoment

Wellendurchmesser bei gegebener Auflagerkraft

da,x = Wellen-AuĂendurchmesser (mm)
M b,x = Biegemoment (Nmm)
Ď b,zul = zulässige Biegespannung (N/mm²)
F a = Auflagerkraft (N)
x = Abstand von der Lagerkraft
da,x = Wellen-AuĂendurchmesser (mm)
M b,x = Biegemoment (Nmm)
Ď b,zul = zulässige Biegespannung (N/mm²)
F a = Auflagerkraft (N)
x = Abstand von der Lagerkraft
nach oben
Wellendurchmesser bei Torsionsbelastung
Allgemeine Torsionsspannungs-Formel

Wellen-AuĂendurchmesser einer Vollwelle bei Torsion

Wellen-AuĂendurchmesser einer Hohlwelle bei Torsion

Widerstandsmoment einer Hohlwelle bei Torsion
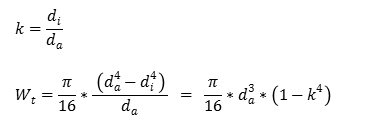
Widerstandsmoment einer Welle bei Torsion mit Passfedernut


Wellen-Innendurchmesser einer Hohlwelle bei Torsion


Ďb = Torsionsspannung (N/mm²)
M t = Torsionsmoment (Nmm)
W t = Widerstandsmoment bei Torsion (mmÂł)
d a = Wellen-AuĂendurchmesser (mm)
d i = Wellen-Innendurchmesser (mm)
Ď t,zul = zulässige Torsionsspannung (N/mm²)
k = Durchmesser-Verhältnis (-)
W t = polares Widerstandsmoment der Welle mit Passfedernut (mm3)
D i = Durchmesser ohne Passfedernut (mm)
Ďb = Torsionsspannung (N/mm²)
M t = Torsionsmoment (Nmm)
W t = Widerstandsmoment bei Torsion (mmÂł)
d a = Wellen-AuĂendurchmesser (mm)
d i = Wellen-Innendurchmesser (mm)
Ď b,zul = zulässige Torsionsspannung (N/mm²)
k = Durchmesser-Verhältnis (-)
W t = polares Widerstandsmoment der Welle mit Passfedernut (mm3)
D i = Durchmesser ohne Passfedernut (mm)
nach oben
Wellendurchmesser bei Biege- und Torsionsbelastung
Vergleichsmoment aus Biege- und Torsionsmoment

Wellen-AuĂendurchmesser bei Vollwellen

Wellen-AuĂendurchmesser bei Hohlwellen

Wellen-Innendurchmesser bei Hohlwellen


Mv = Vergleichsmoment aus Biege- und Torsionsmoment (Nmm)
M b = Biegemoment (Nmm)
M t = Torsionsmoment (Nmm)
Ď b,zul = zulässige Biegespannung (N/mm²)
Ď b,zul = zulässige Torsionsspannung (N/mm²)
Ď = Faktor fĂźr Festigkeitshyphothese
NH = 1 - SH = 2 - GEH = 1,73
d a = Wellen-AuĂendurchmesser (mm)
d i = Wellen-Innendurchmesser (mm)
k = Durchmesser-Verhältnis (-)
Mv = Vergleichsmoment aus Biege- und Torsionsmoment (Nmm)
M b = Biegemoment (Nmm)
M t = Torsionsmoment (Nmm)
Ď b,zul = zulässige Biegespannung (N/mm²)
Ď b,zul = zulässige Torsionsspannung (N/mm²)
Ď = Faktor fĂźr Festigkeitshyphothese
NH = 1 - SH = 2 - GEH = 1,73
d a = Wellen-AuĂendurchmesser (mm)
d i = Wellen-Innendurchmesser (mm)
k = Durchmesser-Verhältnis (-)
nach oben
Verdrehung
Verdrehung bei Torsionsbelastung
Verdrehwinkel einer glatten Welle

Verdrehwinkel bei abgesetzten Wellen

Bogenlänge

Scherwinkel

Wellen-AuĂendurchmesser wenn Ď = 0,25° je m Wellenlänge

Wellen-AuĂendurchmesser bei maximaler Verdrehung


Ď = Verdrehwinkel (°)
M t = Torsionsmoment (Nmm)
Ď t = Torsionsspannung (N/mm²)
G = Schubmodul (N/mm²)
b = Bogenlänge (mm)
γ = Scherwinkel (°)
W p = polares Widerstandsmoment (mm3)
d a = Wellen-AuĂendurchmesser (mm)
r = da / 2 = Wellenradius (mm)
L = Wellenlänge (mm)
I t = polares Flächenträgheitsmoment (mm4)
k A = Anwendungsfaktor (-)
P = Nennleistung der Welle (W)
n = Wellendrehzahl (U/min)
Ď = Verdrehwinkel (°)
M t = Torsionsmoment (Nmm)
Ď t = Torsionsspannung (N/mm²)
G = Schubmodul (N/mm²)
b = Bogenlänge (mm)
γ = Scherwinkel (°)
W p = polares Widerstandsmoment (mm3)
d a = Wellen-AuĂendurchmesser (mm)
r = da / 2 = Wellenradius (mm)
L = Wellenlänge (mm)
I t = polares Flächenträgheitsmoment (mm4)
k A = Anwendungsfaktor (-)
P = Nennleistung der Welle (W)
n = Wellendrehzahl (U/min)
nach oben
Zulässige Verformungen
Zulässige Durchbiegung und Verdrehung fßr Wellen und Achsen
| max. Durchbiegung |
| Wellen und Achsen allgemein, f max bezogen auf Stßtzlänge (Biegung) |
f max â 0,33 mm/m |
| Wellen und Achsen im Maschinenbau |
f max â 0,3 mm/m |
| Wellen und Achsen im Werkzeugmaschinenbau |
f max â 0,2 mm/m |
| Wellen und Achsen im Landmaschinenbau |
f max â 0,5 mm/m |
| Wellen von Elektromotoren - xl=Luftspalt |
f max â 0,2...0,3 *xL |
| Wellen mit Zahnrad an Eingriffsstelle - m=Normalmodul |
f max â 0,005*m |
| Schneckenwelle an Eingriffsstelle - dm=Mittelkreisdurchmesser |
f max â 0,001*dm |
| max. Neigung |
| Gleitlager einstellbar |
tan β max â 10*10-4 |
| Gleitlager einstellbar |
tan β max â 10*10-4 |
| Gleitlager nicht einstellbar |
tan β max â 3*10-4 |
| Wälzlager, Radial-Rillenkugellager |
tan β max â 10*10-4 |
| Wälzlager, Radial-Zylinderrollenlager |
tan β max â 2*10-4 |
| Wellen mit ungehärtetem Zahnrad an Eingriffsstelle |
tan β max â 1*10-4 |
| Wellen mit gehärtetem Zahnrad an Eingriffsstelle |
tan β max â 1*10-4 |
| Industriegetriebe schwere Anwendung - Modul = 5 oder Zahnbreite = 50 mm |
tan β max â 4*10-4 |
| Industriegetriebe schwere Anwendung - Modul > 5 oder Zahnbreite > 50 mm |
tan β max â 1,5*10-4 |
| max. Verdrehung |
| Wellen allgemein, Ď max bezogen auf Verdrehlänge (Torsion) |
Ď max â 0,25°/m |
| Lagerabstand |
| Lagerabstand bei gegebenem Wellendurchmesser |
L = 300...400 * d 0,5 |
nach oben
Wellendurchmesser bzw. Lagerabstand bei zul. Durchbiegung
Der erforderliche Wellendurchmesser bzw. Lagerabstand kann berechnet werden unter der Annahme, einer frei aufliegenden Welle mit einer Punktlast in der
Mitte der Welle und durchgehendem gleichen Durchmesser.
Erforderlicher Wellendurchmesser

Erforderlicher Wellendurchmesser bei E-Modul 210000 N/mm²

Erforderlicher Lagerabstand

Erforderlicher Lagerabstand bei E-Modul 210000 N/mm²

d = Wellendurchmesser (mm)
F = Belastung in der Mitte der Welle (N)
l = Lagerabstand (mm)
E = E-Modul (N/mm²)
f zul = zul. Wellendurchbiegung (mm/m) - siehe Tabelle oben
d = Wellendurchmesser (mm)
F = Belastung in der Mitte der Welle (N)
l = Lagerabstand (mm)
E = E-Modul (N/mm²)
f zul = zul. Wellendurchbiegung (mm/m) - siehe Tabelle oben
nach oben
Nabenabmessungen
Richtwerte fĂźr Wellen-Nabenverbindungen
d = Wellendurchmesser
| VerÂbindungsÂart |
NabenÂauĂenÂdurchmesser |
NabenÂlänge |
| GrauÂguss |
Stahl, GS |
GrauÂguss |
Stahl, GS |
| PassÂfederÂverbindung |
2,0...2,2 * d |
1,8...2,0 * d |
1,6...2,1 * d |
1,1...1,4 * d |
| Keilwelle, Zahnwelle |
1,8...2,0 * d |
1,8...2,0 * d |
1,0...1,3 * d |
0,6...0,9 * d |
| LängsÂbewegliche Nabe |
1,8...2,0 * d |
1,6...1,8 * d |
2,0...2,2 * d |
1,8...2,0 * d |
| PolygonÂverbindung |
1,6...1,8 * d |
1,3...1,6 * d |
1,8...2,0 * d |
1,6...1,8 * d |
| PressÂverband |
2,2...2,6 * d |
2,0...2,5 * d |
1,2...1,5 * d |
0,8...1,0 * d |
| Spann-, Klemm-, KeilÂverbindung |
2,0...2,2 * d |
1,8...2,0 * d |
1,6...2,0 * d |
1,2...1,5 * d |
nach oben
Kerbformzahl - Kerbwirkungszahl
Berechnung Kerbformzahl Flachstab
Berechnungsprogramm zur Berechnung der Kerbformzahl fĂźr einen Flachstab, mit verschiedene Geometrien und Belastungsarten.
nach oben
Berechnung Kerbformzahl Rundstab
Berechnungsprogramm zur Berechnung der Kerbformzahl fĂźr einen Rundstab, mit verschiedene Geometrien und Belastungsarten.
nach oben
Kerbwirkungszahl
Zur Auslegung dynamisch beanspruchter Bauteile wird die Kerbwirkungszahl βk als Verhältnis der Dauerfestigkeit ĎD eines glatten, polierten Stabes zur
Dauerfestigkeit ĎDk der glatten gekerbten Probe herangezogen. Die Kerbwirkungszahl βk ist abhängig von der Beanspruchungsart, der Kerbform sowie vom Werkstoff und wird
experimentell ermittelt.
Kerbwirkungszahlen
Berechnungsprogramm zur Berechnung der Kerbwirkungszahl fĂźr verschiedene Geometrien und Belastungsarten.

Rundstab abgesetzt
|

Rundstab mit Rundkerbe
|

Sicherungsring Nut
|

Rundstab mit Passfesder
|

Rundstab mit Pressverbindung
|
| Kerbform |
|
Biegung
βkb |
Torsion
βkt |
| QuerÂbohrung |
 |
1,7...2,0
d/D=0,14 |
1,7...2.0
d/d=0,14 |
| PassÂfedernut |
 |
1,8...2,5 |
1,3...2,2 |
| AusÂlaufnut |
 |
1,3...1,5 |
1,3...2,2 |
| KeilÂwelle parallele Flanken |
|
1,4...2,3 |
1,9...3,1 |
| KerbÂzahnÂwellen |
|
1,6...2,6 |
1,9...3,1 |
| KegelÂspannringe |
|
1,6 |
1,4 |
nach oben
Einflussfaktoren auf die Dauerfestigkeit
Einflussfaktoren auf die Dauerfestigkeit
Bei der Berechnung der Dauerfestigkeit eines Bauteils sind verschiedene Einflussfaktoren zu berĂźcksichtigen:
- Technologischer GrĂśĂeneinflussfaktor K1
Der Faktor K1 berßcksichtigt, dass die erreichbare Härte beim Vergßten bzw. Einsatzhärten mit steigendem Durchmesser abnimmt.
- Geometrischer GrĂśĂeneinflussfaktor K2
Der geometrische GrĂśĂeneinflussfaktor K2 berĂźcksichtigt, dass bei grĂśĂer werdendem Durchmesser oder Dicken die Biegewechselfestigkeit in die Zug/Druckwechselfestigkeit
Ăźbergeht und analog auch die Torsionswechselfestigkeit sinkt.
Berechnung von:
- Technologischer GrĂśĂeneinflussfaktor K1
- Geometrischer GrĂśĂeneinflussfaktor K2
nach oben
Einflussfaktor Oberflächenrauigkeit
Der Einflussfaktor Kf der Oberflächenrauheit, berßcksichtigt den zusätzlichen Einfluss der Rauheit auf die Ürtlichen Spannungen und damit auf die Dauerfestigkeit
des Bauteils.
Zug-Druck und Biegung


Torsion

KfĎ = Zug-Druck Oberflächenrauigkeitsfaktor (-)
K fĎ = Torsion Oberflächenrauigkeitsfaktor (-)
Ď b(deff) = Zugfestigkeit (N/mm²)
Rz = mittl. Rauigkeit (Îźm)
bei Walzhaut Rz=200 Îźm
Ď B(dB) = Zugfestigkeit Bezugsdurchmesser (N/mm²)
K1 (deff) = Technologischer Einflussfaktor (-)
KfĎ = Zug-Druck Oberflächenrauigkeitsfaktor (-)
K fĎ = Torsion Oberflächenrauigkeitsfaktor (-)
Ď b(deff) = Zugfestigkeit (N/mm²)
Rz = mittl. Rauigkeit (Îźm)
bei Walzhaut Rz=200 Îźm
Ď B(dB) = Zugfestigkeit Bezugsdurchmesser (N/mm²)
K1 (deff) = Technologischer Einflussfaktor (-)
nach oben
Einflussfaktor fßr Oberflächenverfestigung Kv
Der Einflussfaktor der Oberflächenverfestigung Kv berßcksichtigt den Einfluss (Eigenspannung, Härte) des veränderten Oberflächenzustandes durch das jeweilige
technologische Verfahren auf die Dauerfestigkeit.
Bei Durchmesser grĂśĂer 40 mm ist Kv = 1.
| OberÂflächenÂverfestigung |
DurÂchmesser |
Kv Faktor |
| Nitrieren |
8...25 |
1,15...1,25 |
| 25...40 |
1,10...1,15 |
| EinsatzÂhärten |
8...25 |
1,20...2,10 |
| 25...40 |
1,10...1,50 |
| KarboÂnitrierÂhärten |
8...25 |
1,10...1,90 |
| 25...40 |
1,00...1,40 |
| Rollen |
7...25 |
1,20...1,40 |
| 25...40 |
1,10...1,25 |
| KugelÂstrahlen |
7...25 |
1,10...1,30 |
| 25...40 |
1,10...1,20 |
InÂduktivÂhärten
FlammÂhärten |
7...25 |
1,20...1,60 |
| 25...40 |
1,10...1,40 |
nach oben
Gesamt-Einflussfaktor
Gesamteinflussfaktor
Zug-Druck und Biegung

Torsion

KĎ = Gesamteinflussfaktor Ď (-)
K Ď = Gesamteinflussfaktor Ď (-)
β Ď = Kerbwirkungszahl Ď (-)
β Ď = Kerbwirkungszahl Ď (-)
K 2 = Geometrischer Einflussfaktor (-)
K f,Ď = Einflussfaktor Oberflächenrauheit Ď (-)
K f,Ď = Einflussfaktor Oberflächenrauheit Ď (-)
K v = Einflussfaktor Oberflächenverfestigung (-)
KĎ = Gesamteinflussfaktor Ď (-)
K Ď = Gesamteinflussfaktor Ď (-)
β Ď = Kerbwirkungszahl Ď (-)
β Ď = Kerbwirkungszahl Ď (-)
K 2 = Geometrischer Einflussfaktor (-)
K f,Ď = Einflussfaktor Oberflächenrauheit Ď (-)
K f,Ď = Einflussfaktor Oberflächenrauheit Ď (-)
K v = Einflussfaktor Oberflächenverfestigung (-)
nach oben
Gestaltfestigkeit
Belastungs- und Spannungsarten
Ď
N = Normalspannung (N/mm²) - Zug/Druck
F
N = Normalkraft (N)
A
= Querschnittsfläche (mm²)
Ď
t = Torsionsspannung (N/mm²)
M
t = Torsionsmoment (Nmm)
W
t = Torsions-Widerstandsmoment (mmÂł)
Ď
b = Biegespannung (N/mm²)
M
b = Biegemoment (Nmm)
W
b = Biege-Widerstandsmoment (mmÂł)
Ď
a = Spannungsamplitude (N/mm²)
Ď
m = Mittelspannung (N/mm²)
Ď
o = Oberspannung (N/mm²)
Ď
u = Unterspannung (N/mm²)

Ď
N = Normalspannung (N/mm²) - Zug/Druck
F
N = Normalkraft (N)
A
= Querschnittsfläche (mm²)
Ď
t = Torsionsspannung (N/mm²)
M
t = Torsionsmoment (Nmm)
W
t = Torsions-Widerstandsmoment (mmÂł)
Ď
b = Biegespannung (N/mm²)
M
b = Biegemoment (Nmm)
W
b = Biege-Widerstandsmoment (mmÂł)
Ď
a = Spannungsamplitude (N/mm²)
Ď
m = Mittelspannung (N/mm²)
Ď
o = Oberspannung (N/mm²)
Ď
u = Unterspannung (N/mm²)

nach oben
Vergleichs-Mittelspannung bei mehrachsiger Beanspruchung
Vergleichs-Mittelspannungen


Ďmv = Vergleichs-Mittelspannung (N/mm²)
Ď mv = Torsion-Vergleichs-Mittelspannung (N/mm²)
Ď zdm = Zug-Druck-Mittelspannung (N/mm²)
Ď bdm = Biege-Mittelspannung (N/mm²)
Ď m = Torsion-Mittelspannung (N/mm²)
Ďmv = Vergleichs-Mittelspannung (N/mm²)
Ď mv = Torsion-Vergleichs-Mittelspannung (N/mm²)
Ď zdm = Zug-Druck-Mittelspannung (N/mm²)
Ď bdm = Biege-Mittelspannung (N/mm²)
Ď m = Torsion-Mittelspannung (N/mm²)
nach oben
Gestalt-Dauerfestigkeit gekerbter Stab - einachsige Beanspruchung
Die Bauteilfestigkeit des gekerbten Stabs, unter BerĂźcksichtigung der o. g. Einflussfaktoren, berechnet sich nach folgenden Formeln:
Zug-Druck-Wechselfestigkeit

Biege-Wechselfestigkeit

Torsions-Wechselfestigkeit

nach oben
Mittelspannungsempfindlichkeit
Zug-Druck

Biegung

Torsion

ĎzdĎK = Mittelspannungsempfindlichkeit Zug-Druck (-)
Ď bĎK = Mittelspannungsempfindlichkeit Biegung (-)
Ď ĎK = Mittelspannungsempfindlichkeit Torsion (-)
Ď zdWK = Zug-Druck Bauteilwechselfestigkeit (N/mm²)
Ď bWK = Biegung Bauteilwechselfestigkeit (N/mm²)
Ď ĎWK = Torsion Bauteilwechselfestigkeit (N/mm²)
Ď B(deff) = Zugfestigkeit bezogen auf deff (N/mm²)
ĎzdĎK = Mittelspannungsempfindlichkeit Zug-Druck (-)
Ď bĎK = Mittelspannungsempfindlichkeit Biegung (-)
Ď ĎK = Mittelspannungsempfindlichkeit Torsion (-)
Ď zdWK = Zug-Druck Bauteilwechselfestigkeit (N/mm²)
Ď bWK = Biegung Bauteilwechselfestigkeit (N/mm²)
Ď ĎWK = Torsion Bauteilwechselfestigkeit (N/mm²)
Ď B(deff) = Zugfestigkeit bezogen auf deff (N/mm²)
nach oben
Spannungsamplitude der Bauteilfestigkeit
Wenn Ďmv bzw. Ďmv konstant
Zug-Druck

Biegung

Torsion
 Wenn Ďmv/Ďzd,ba bzw. Ďmv/ĎĎa konstant
Wenn Ďmv/Ďzd,ba bzw. Ďmv/ĎĎa konstant
Zug-Druck

Biegung

Torsion

ĎzdADK = Zug-Druck Bauteilausschlagfestigkeit (N/mm²)
Ď bADK = Biege Bauteilausschlagfestigkeit (N/mm²)
Ď ĎADK = Torsion Bauteilausschlagfestigkeit (N/mm²)
Ď zdWK = Zug-Druck Bauteilwechselfestigkeit (N/mm²)
Ď bWK = Biege Bauteilwechselfestigkeit (N/mm²)
Ď ĎWK = Torsion Bauteilwechselfestigkeit (N/mm²)
Ď zdĎK = Mittelspannungsempfindlichkeit Zug-Druck (-)
Ď bĎK = Mittelspannungsempfindlichkeit Biegung (-)
Ď ĎK = Mittelspannungsempfindlichkeit Torsion (-)
Ď mv = Vergleichs-Mittelspannung (N/mm²)
Ď mv = Torsion Vergleichs-Mittelspannung (N/mm²)
Ď zda = Zug-Druck Ausschlagspannung aus der Beanspruchung (N/mm²)
Ď ba = Biege-Ausschlagspannung aus der Beanspruchung (N/mm²)
Ď Ďa = Torsion-Ausschlagspannung aus der Beanspruchung (N/mm²)
ĎzdADK = Zug-Druck Bauteilausschlagfestigkeit (N/mm²)
Ď bADK = Biege Bauteilausschlagfestigkeit (N/mm²)
Ď ĎADK = Torsion Bauteilausschlagfestigkeit (N/mm²)
Ď zdWK = Zug-Druck Bauteilwechselfestigkeit (N/mm²)
Ď bWK = Biege Bauteilwechselfestigkeit (N/mm²)
Ď ĎWK = Torsion Bauteilwechselfestigkeit (N/mm²)
Ď zdĎK = Mittelspannungsempfindlichkeit Zug-Druck (-)
Ď bĎK = Mittelspannungsempfindlichkeit Biegung (-)
Ď ĎK = Mittelspannungsempfindlichkeit Torsion (-)
Ď mv = Vergleichs-Mittelspannung (N/mm²)
Ď mv = Torsion Vergleichs-Mittelspannung (N/mm²)
Ď zda = Zug-Druck Ausschlagspannung aus der Beanspruchung (N/mm²)
Ď ba = Biege-Ausschlagspannung aus der Beanspruchung (N/mm²)
Ď Ďa = Torsion-Ausschlagspannung aus der Beanspruchung (N/mm²)
nach oben
Sicherheit gegen ErmĂźdungsbruch
Ausschlagspannung aus der Beanspruchung

Sicherheit

- nur Biegung

- nur Torsion

Ďa = Ausschlagspannung (N/mm²)
Ď o = Oberspannung (N/mm²) - max. Spannung
Ď u = Unterspannung (N/mm²) - min. Spannung
Ď zda = Zug-Druck-Ausschlagspannung (N/mm²)
Ď ba = Biege-Ausschlagspannung (N/mm²)
Ď Ďa = Torsion-Ausschlagspannung (N/mm²)
Ď zdADK = Zug-Druck Bauteilausschlagfestigkeit (N/mm²)
Ď bADK = Biege Bauteilausschlagfestigkeit (N/mm²)
Ď ĎADK = Torsion Bauteilausschlagfestigkeit (N/mm²)
S = Sicherheit gegen ErmĂźdungsbruch (-)
Ďa = Ausschlagspannung (N/mm²)
Ď o = Oberspannung (N/mm²) - max. Spannung
Ď u = Unterspannung (N/mm²) - min. Spannung
Ď zda = Zug-Druck-Ausschlagspannung (N/mm²)
Ď ba = Biege-Ausschlagspannung (N/mm²)
Ď Ďa = Torsion-Ausschlagspannung (N/mm²)
Ď zdADK = Zug-Druck Bauteilausschlagfestigkeit (N/mm²)
Ď bADK = Biege Bauteilausschlagfestigkeit (N/mm²)
Ď ĎADK = Torsion Bauteilausschlagfestigkeit (N/mm²)
S = Sicherheit gegen ErmĂźdungsbruch (-)
nach oben
Kritische Drehzahl
Biegeeigenfrequenz [1]
Die auf die Welle wirkenden zusätzlichen Belastungen (Zahnkräfte, Querkräfte usw.) sind bei der Biegesteifigkeit der Welle nicht zu berßcksichtigen.
Ď = Winkelgeschwindigkeit (rad/s)
C = Biegesteifigkeit der Welle (N/m)
m = Einzelmasse (Scheibe) (kg)
f k = Kritische Eigenfrequenz (Hz)
F G = Gewichtskraft der Einzelmasse (N)
f G = Durchbiegung der Welle durch die Einzelmasse (m)
g = Erdbeschleunigung 9,81 (m/s²)
n k = Kritische Drehzahl (1/min)
E = E-Modul (N/mm²)
I = Biege-Trägheitsmoment (mm4)
L = Lagerabstand (mm)
a = Abstand Masse zum Lager (mm)
b = Abstand Masse zum Lager (mm)
Ď = Winkelgeschwindigkeit (rad/s)
C = Biegesteifigkeit der Welle (N/m)
m = Einzelmasse (Scheibe) (kg)
f k = Kritische Eigenfrequenz (Hz)
F G = Gewichtskraft der Einzelmasse (N)
f G = Durchbiegung der Welle durch die Einzelmasse (m)
g = Erdbeschleunigung 9,81 (m/s²)
n k = Kritische Drehzahl (1/min)
E = E-Modul (N/mm²)
I = Biege-Trägheitsmoment (mm4)
L = Lagerabstand (mm)
a = Abstand Masse zum Lager (mm)
b = Abstand Masse zum Lager (mm)