Berechnung der Schallpegel, Schallwerte und des Strömungsrauschens
Hinweis
In dieser Formelsammlung steht fĂŒr die Funktion log der Zehnerlogarithmus, z. B. log(100) = 2
Heute wird der Zehnerlogarithmus auch mit der Funktion lg oder lg10 bezeichnet.
Der natĂŒrliche Logarithmus ist mit der Funktion ln bezeichnet, z. B. ln(2) = 0,693.
SchallpegelÀnderung
Entfernungsbedingte Pegelabnahme - Punktschallquelle - Theorie
Mit zunehmender Entfernung von der Schallquelle wird ein GerÀusch schwÀcher.
Bei einer Punktschallquelle und der Annahme einer kugelförmigen Schallausbreitung ergibt sich die Abnahme des Schallpegels somit zu:
Î L p = Schallpegelabnahme zwischen Standort 1 und 2 (dB)
L p1 = Schallpegel am Standort 1 (dB)
L p2 = Schallpegel am Standort 2 (dB)
r 1 = Entfernung zur Schallquelle am Standort 1 (m)
r 2 = Entfernung zur Schallquelle am Standort 2 (m)
Î L p = Schallpegelabnahme zwischen Standort 1 und 2 (dB)
L p1 = Schallpegel am Standort 1 (dB)
L p2 = Schallpegel am Standort 2 (dB)
r 1 = Entfernung zur Schallquelle am Standort 1 (m)
r 2 = Entfernung zur Schallquelle am Standort 2 (m)
Die Schallpegelabnahme bei Entfernungsverdoppelung bei einer Punktschallquelle betrÀgt nach der Theorie 6 dB.
nach oben
Entfernungsbedingte Pegelabnahme - Punktschallquelle - Praxiswert
Bei der Schallpegelabnahme im Freifeld sind weitere wesentliche EinflĂŒsse zu berĂŒcksichtigen:
- BodendÀmpfung
- Luftabsorption
- Metrologische EinflĂŒsse (Temperatur, Wind usw.)
Um diese EinflĂŒsse zu berĂŒcksichtigen hat sich in der Praxis gezeigt, dass mit einer Schallpegelabnahme bei Entfernungsverdoppelung von 5
dB zu rechnen ist.
Î L p = Schallpegelabnahme zwischen Standort 1 und 2 (dB)
L p1 = Schallpegel am Standort 1 (dB)
L p2 = Schallpegel am Standort 2 (dB)
r 1 = Entfernung zur Schallquelle am Standort 1 (m)
r 2 = Entfernung zur Schallquelle am Standort 2 (m)
Î L p = Schallpegelabnahme zwischen Standort 1 und 2 (dB)
L p1 = Schallpegel am Standort 1 (dB)
L p2 = Schallpegel am Standort 2 (dB)
r 1 = Entfernung zur Schallquelle am Standort 1 (m)
r 2 = Entfernung zur Schallquelle am Standort 2 (m)
nach oben
Entfernungsbedingte Pegelabnahme - Linienschallquellen
Im Gegensatz zur Punktschallquelle, bei der man von einer kugelförmigen Ausbreitung der Schallwellen ausgeht, breiten sich bei sehr
langen Linienschallquellen (z. B. Eisenbahnzug, Autokolonne, Rohrleitung) die Schallwellen auf einer Zylinder-oberflÀche aus.
Î L p = Schallpegelabnahme zwischen Standort 1 und 2 (dB)
L p1 = Schallpegel am Standort 1 (dB)
L p2 = Schallpegel am Standort 2 (dB)
r 1 = Entfernung zur Schallquelle am Standort 1 (m)
r 2 = Entfernung zur Schallquelle am Standort 2 (m)
Î L p = Schallpegelabnahme zwischen Standort 1 und 2 (dB)
L p1 = Schallpegel am Standort 1 (dB)
L p2 = Schallpegel am Standort 2 (dB)
r 1 = Entfernung zur Schallquelle am Standort 1 (m)
r 2 = Entfernung zur Schallquelle am Standort 2 (m)
Die Schallpegelabnahme bei Entfernungsverdoppelung einer Linienschallquellen betrÀgt 3 dB.
nach oben
Schallpegelerhöhung bei mehreren gleichlauten Schallquellen
Wirken mehrere Schallquellen gleicher LautstÀrke nebeneinander, erhöht sich der Schalldruckpegel um folgende Werte:
L pges = Schalldruckpegel gesamt (dB)
L pi = Schalldruckpegel der Einzelquellen (dB)
n = Anzahl gleichlauter Schallquellen
ΠL p = Schallpegelerhöhung (dB)
L pges = Schalldruckpegel gesamt (dB)
L pi = Schalldruckpegel der Einzelquellen (dB)
n = Anzahl gleichlauter Schallquellen
ΠL p = Schallpegelerhöhung (dB)
| Anzahl SchallÂquellen |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| SchallÂpegelÂerÂhöhung (dB) |
3,0 |
4,8 |
6,0 |
7,0 |
7,8 |
8,5 |
9,0 |
9,5 |
10,0 |
10,4 |
10,8 |
nach oben
Summenpegel von mehreren ungleichlauten Schallquellen
Bei der Ermittlung des Gesamtschallpegels von mehreren Schallquellen mit unterschiedlichen Schallpegeln ist der Schallpegel wie folgt
zu ermitteln:
L pges = Gesamtschalldruckpegel (dB)
L pi = Schalldruckpegel einer Schallquelle (dB)
n = Anzahl Schallquellen
L pges = Gesamtschalldruckpegel (dB)
L pi = Schalldruckpegel einer Schallquelle (dB)
n = Anzahl Schallquellen
Schallpegelerhöhung der lauteren Schallquelle , bei zwei Schallquellen mit unterschiedlichen Schallpegeln.
SchallÂpegelÂdifferenz
zweier SchallÂquellen (dB) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
SchallÂpegelÂerhöhung der
lauteren SchallÂquelle(dB) |
3,0 |
2,5 |
2,1 |
1,8 |
1,5 |
1,2 |
1,0 |
0,8 |
0,6 |
0,5 |
0,4 |
nach oben
Energetische Mittelwertbildung von mehreren Schallquellen
L m = Mittelwert-Schalldruckpegel (dB)
L pi = Schalldruckpegel einer Schallquelle (dB)
n = Anzahl Schallquellen
L m = Mittelwert-Schalldruckpegel (dB)
L pi = Schalldruckpegel einer Schallquelle (dB)
n = Anzahl Schallquellen
nach oben
ZulĂ€ssige Ăberschreitung des Mittelungspegels bei zeitlich begrenztem Betrieb
Bei einem Schallpegel treten oftmals unterschiedliche Schallpegelwerte ĂŒber einen gewissen Zeitraum auf, oder die Einwirkzeit wirkt
nicht ĂŒber die gesamte Tages- oder Nachtzeit. Die Schallpegel werden dann nach ihren zeitlichen Anteilen nach der Energetischen
Mittelwertbildung summiert, so dass eine Pegelerhöhung fĂŒr einzelne Zeitintervalle möglich ist.
Die Summe aus der zeitlichen Betrachtung darf den zulĂ€ssigen Schallpegel nicht ĂŒberschreiten. Die Schallpegelerhöhung ist nach Tageszeit
max. 16 Std. und Nachtzeit max. 8 Std. getrennt zu betrachten.
L p ges = Mittelungspegel (dB)
L pi = Schalldruckpegel wÀhrend des Zeitintervalls t i (dB)
ÎL p = SchallpegelĂŒberschreitung (dB)
T ges = zu betrachtende Gesamtzeit (Std.)
t i = Zeitintervall fĂŒr Schalldruckpegel L pi (Std).
n = Anzahl Zeitintervalle (-)
L p ges = Mittelungspegel (dB)
L pi = Schalldruckpegel wÀhrend des Zeitintervalls t i (dB)
ÎL p = SchallpegelĂŒberschreitung (dB)
T ges = zu betrachtende Gesamtzeit (Std.)
t i = Zeitintervall fĂŒr Schalldruckpegel L pi (Std).
n = Anzahl Zeitintervalle (-)
Ăberschreitung des Schallpegels bei zeitlich begrenztem Betrieb.
| ZeitÂinterÂvall von L pi (Std.) |
|
16 |
12 |
10 |
8 |
6 |
5 |
4 |
3 |
2 |
1 |
| ĂberÂschreitung (dB) |
tags |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
12 |
| ĂberÂschreitung (dB) |
nachts |
|
|
|
0 |
1 |
2 |
3 |
4 |
6 |
9 |
Faustformel: Eine Halbierung (Verdoppelung) der Einwirkungszeit eines GerÀusches vermindert (erhöht) seinen Mittelungspegel um ca. 3
dB.
nach oben
Störpegel
Subtraktion von Schallpegeln - Berechnung des Schallpegels ohne Störpegel
Die Subtraktion von Schallpegeln wird bei folgenden Auswertungen bzw. Berechnungen angewendet:
Messung einer Schallquelle
Bei der Messung einer Schallquelle wird ein Gesamtpegel gemessen der sich aus der zu messenden Schallquelle und einem UmgebungsgerÀusch
(Störpegel) ergibt. Um eine Aussage ĂŒber den absoluten Schallpegel (L Nutz) der zu messenden Schallquelle machen zu können, ist die
Subtraktion von Schallpegeln anzuwenden. In AbhĂ€ngigkeit der Differenz zwischen Gesamt- und Störpegel ist der unten aufgefĂŒhrte
Korrekturpegel vom Gesamtpegel abzuziehen. Das Ergebnis ist der Schallpegel der zu messenden Schallquelle. BetrÀgt die Differenz zwischen
Gesamt- und Störpegel mehr als 10 dB, kann die Pegelsubtraktion entfallen, da der Gesamtpegel dem Schallpegel der zu messenden
Schallquelle entspricht.
Berechnung des Nutzpegels
Bei der Auslegung von SchalldĂ€mpfern ist eine zulĂ€ssige Schallforderung gegeben (L ges). Sind mehrere Schallquellen zu berĂŒcksichtigen (L
Stör), so kann mit der Schallpegelsubtraktion der zulÀssige Nutzpegel der letzten Schallquelle berechnet werden, so dass der
Gesamtschallpegel nicht ĂŒberschritten wird.
L Stör = Störpegel (dB)
L Nutz = Nutzpegel (dB)
L ges = Gesamtschalldruckpegel (dB)
L Kor = Korrekturpegel (dB)
L Stör = Störpegel (dB)
L Nutz = Nutzpegel (dB)
L ges = Gesamtschalldruckpegel (dB)
L Kor = Korrekturpegel (dB)
Bei einer Pegeldifferenz zwischen Gesamt- und Störpegel ist folgender Korrekturschallpegel vom Gesamtschallpegel abzuziehen.
| L ges - L Stör (dB) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| L kor (dB) |
6,87 |
4,33 |
3,02 |
2,20 |
1,65 |
1,26 |
0,97 |
0,75 |
0,58 |
0,46 |
0,36 |
nach oben
Korrekturschallpegel bei Messungen mit Störpegel
Bei Schallpegelmessungen wird ein Gesamtpegel gemessen der sich aus der zu messenden Schallquelle und einem UmgebungsgerÀusch
(Störpegel) ergibt. Um die zu messende Schallquelle beurteilen zu können, ist der der unten dargestellte Korrekturschallpegel vom
Gesamtpegel zu Subtraktieren. BetrÀgt die Differenz zwischen Nutzpegel und Störpegel mehr als 10 dB, kann die Pegelsubtraktion entfallen.
L ges = Gesamtschallpegel (dB) - L Stör = Störpegel (dB) - L Kor =
Korrekturschallpegel (dB) L Mess = Messpegel der zu messenden Schallquelle (dB) - L Mess = L
ges - L Kor
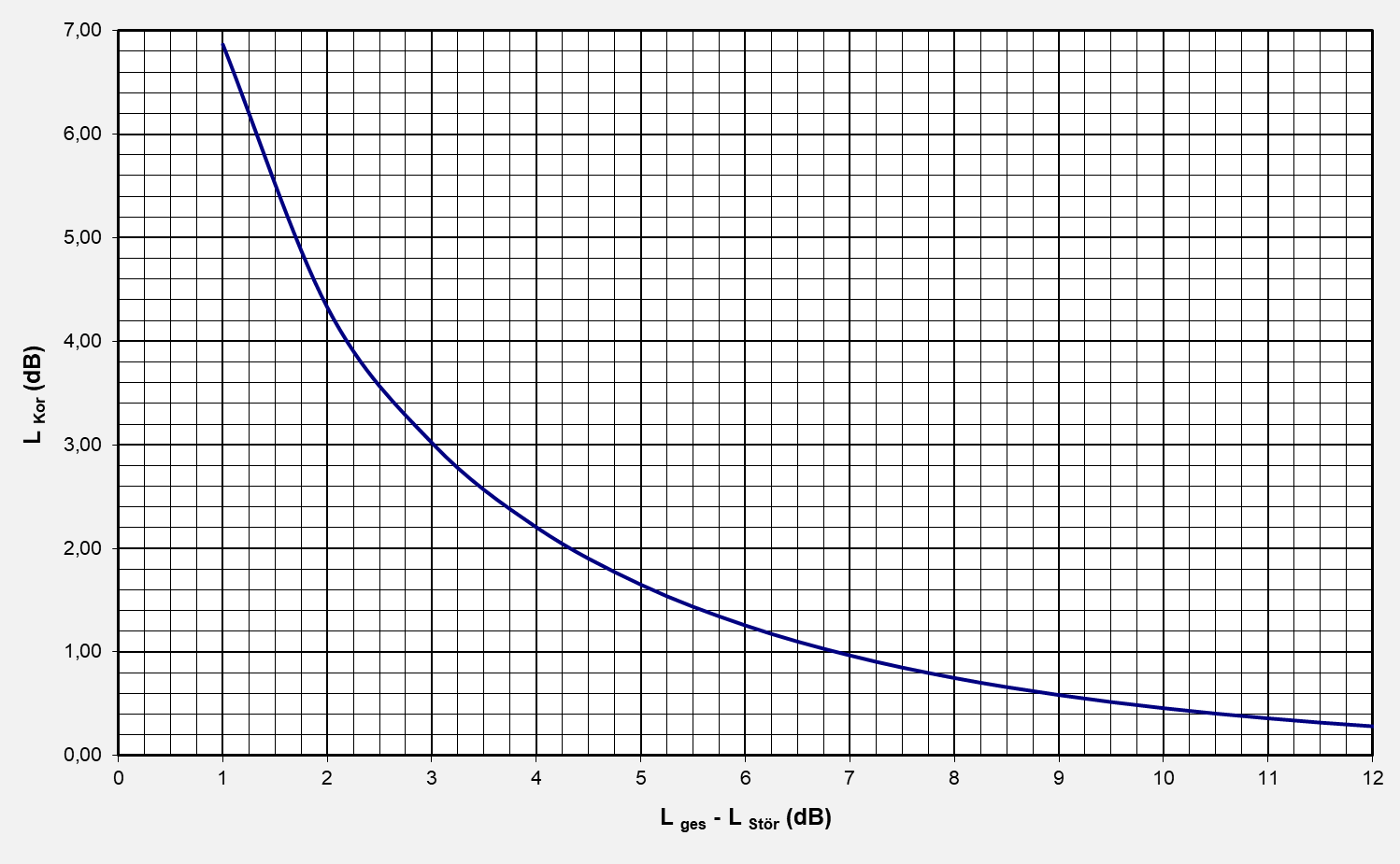
Beispiel:
L ges = Gesamtschallpegel = 60 (dB)
L Stör = Störpegel = 56 (dB)
Differenz L ges - L Stör = 60 - 56 = 4 (dB)
L Kor = Korrekturschallpegel nach Diagramm = 2,2 (dB)
L Mess = Messpegel der zu messenden Schallquelle (dB) - L Mess = L ges - L Kor =
60 - 2,2 = 57,8 (dB)
Die Bezugswerte sind die Hörschwelle fĂŒr das menschliche Gehör, sie entsprechen einem Schalldruckpegel von 0 dB.
nach oben
Schallwerte
Schalldruckpegel
Eine der zentralen GröĂen in der Akustik ist der Schalldruckpegel, der zur Beschreibung der LautstĂ€rke benötigt wird.
Dieser ist als logarithmisches MaĂ fĂŒr das VerhĂ€ltnis zwischen dem gemessenen Schalldruck und einem Bezugsschalldruck definiert.
Schalldruck

Bezugs-Schalldruck

Schalldruckpegel

p â = Schalldruck (Pa)
p 0 = Bezugs-Schalldruck (Pa)
L p = Schalldruckpegel (dB)
p â = Schalldruck (Pa)
p 0 = Bezugs-Schalldruck (Pa)
L p = Schalldruckpegel (dB)
nach oben
SchallintensitÀtspegel
Die SchallintensitĂ€t, die zu den SchallenergiegröĂen gehört, bezeichnet die Schallleistung, die je FlĂ€cheneinheit durch eine
durchschallte FlÀche tritt.
Die zugehörige logarithmische GröĂe ist der SchallintensitĂ€tspegel.
Zwei inkohĂ€rente Schallquellen ergeben eine SchallintensitĂ€tspegel-Zunahme um 3 dB gegenĂŒber einer Schallquelle.
SchallintensitÀt

Bezugs-SchallintensitÀt

SchallintensitÀtspegel

I â = SchallintensitĂ€t (W/mÂČ)
I 0 = Bezugs-SchallintensitĂ€t (W/mÂČ)
L I = SchallintensitÀtspegel (dB)
I â = SchallintensitĂ€t (W/mÂČ)
I 0 = Bezugs-SchallintensitĂ€t (W/mÂČ)
L I = SchallintensitÀtspegel (dB)
nach oben
Schallschnellepegel
Die Schallschnelle v ist die zeitliche Ableitung der Schallauslenkung. Im Schallfeld ist sie eine vektorielle GröĂe. Sie gibt die
Wechselgeschwindigkeit des schwingenden Teilchens im Medium an. Im europĂ€ischen Raum wird fĂŒr die Schallschnelle ein Bezugswert v0 =
5·10-8 m/s beim Schalldruck von 20 ”Pa verwendet.
Die Schallschnelle in Luft bei einem Schalldruck von 0,1 Pa gleich einem Schalldruckpegel von 74 dB errechnet sich zu 0,25 mm/s, wobei
die Schallgeschwindigkeit rund 340 m/s betrÀgt.
Schallschnelle

Bezugs-Schallschnelle

Schallschnellepegel

Îœ â = Schallschnelle (m/s)
Μ 0 = Bezugs-Schallschnelle (m/s)
L Μ = Schallschnellepegel (dB)
Îœ â = Schallschnelle (m/s)
Μ 0 = Bezugs-Schallschnelle (m/s)
L Μ = Schallschnellepegel (dB)
nach oben
Schallenergie
Die Schallenergie ist als SchallenergiegröĂe die Summe der in einem Schallfeld enthaltenen potentiellen und kinetischen Energie.
Die Schallwellen transportieren die Schallenergie von der Schallquelle weg in den umgebenden Raum. Die gesamte Energie, die von einer
Schallquelle innerhalb von einer Sekunde abgestrahlt wird, heiĂt Schallleistung, die in Watt gemessen wird,
Schallenergie

Bezugs-Schallenergie

Schallenergiepegel

W â = Schallenergie (J)
W 0 = Bezugs-Schallenergie (J)
L W = Schallenergiepegel (dB)
W â = Schallenergie (J)
W 0 = Bezugs-Schallenergie (J)
L W = Schallenergiepegel (dB)
nach oben
Schallenergiedichte
Die Schallenergiedichte (Formelzeichen E oder w) ist ein MaĂ zur Beschreibung der an einem bestimmten Ort des Schallfelds vorhandenen
Schallenergie.
Sie ist eine SchallenergiegröĂe. Die zugehörige logarithmische GröĂe ist der Schallenergiedichtepegel.
Schallenergiedichte

Bezugs-Schallenergiedichte

Schallenergiedichtepegel

W â = Schallenergiedichte (J/mÂł)
W 0 = Bezugs-Schallenergiedichte (J/mÂł)
L W = Schallenergiedichtepegel (dB)
W â = Schallenergiedichte (J/mÂł)
W 0 = Bezugs-Schallenergiedichte (J/mÂł)
L W = Schallenergiedichtepegel (dB)
nach oben
Frequenz
Die Frequenz f bezeichnet die Anzahl der Schwingungen pro Sekunde, stellt also eine WiederholungshÀufigkeit dar (Hertz: Hz =
Schwingung/s).
f â = Frequenz (1/s - Hz)
T â = Periodendauer (s)
Infraschall < 16 Hz nicht hörbar
Hörschall von 16 Hz bis 20 kHz hörbar
Ultraschall von 20 kHz bis 1,6 GHz nicht hörbar
Hyperschall > 1 GHz nicht hörbar
f â = Frequenz (1/s - Hz)
T â = Periodendauer (s)
Infraschall < 16 Hz nicht hörbar
Hörschall von 16 Hz bis 20 kHz hörbar
Ultraschall von 20 kHz bis 1,6 GHz nicht hörbar
Hyperschall > 1 GHz nicht hörbar
nach oben
WellenlÀnge
Die WellenlÀnge λ ist in einer sich ausbreitenden Welle der Abstand zwischen zwei aufeinander folgenden Punkten des gleichen
Schwingungszustandes, also z. B. zwischen zwei Maxima oder zwei Minima.
Eine Periode ist die zeitliche Dauer eines vollstÀndigen Bewegungszyklus, nach dem wieder der gleiche Bewegungszustand erreicht wird.
WellenlÀnge

Periodendauer

λ â = WellenlĂ€nge (m)
c â = Schallgeschwindigkeit (m/s)
f â = Frequenz (1/s - Hz)
T â = Periodendauer (s)
λ â = WellenlĂ€nge (m)
c â = Schallgeschwindigkeit (m/s)
f â = Frequenz (1/s - Hz)
T â = Periodendauer (s)
nach oben
Schallgeschwindigkeit
Die Schallgeschwindigkeit ist die Geschwindigkeit, mit der sich eine Schallwelle ausbreitet, sie ist abhÀngig von Art und Zustand des
Mediums.
Luft


NĂ€herungsformel

Ideale Gase

FlĂŒssigkeiten

Feststoffe

c
â = Schallgeschwindigkeit (m/s)
Îș
â = Adiabatenexponent (-) - Luft=1,4
R
= Gaskonstante (J/(kg*K) - Luft=287
T
= Absoluttemperatur (K)
p
â = Gasdruck (Pa)
t
â = Temperatur (°C)
Ï
â = Dichte (kg/mÂł)
M
â = Molare Masse (kg/mol)
K
â = Kompressionsmoduls (Pa)
c
log = Longitudinale Schallgeschwindigkeit (m/s)
c
trans = Transversale Schallgeschwindigkeit (m/s)
E
â = ElastizitĂ€tsmodul (N/mÂČ) (°C)
Μ
â = Poissonzahl (-)
Schallgeschwindigkeit verschiedener Stoffe
c
â = Schallgeschwindigkeit (m/s)
Îș
â = Adiabatenexponent (-) - Luft=1,4
R
= Gaskonstante (J/(kg*K) - Luft=287
T
= Absoluttemperatur (K)
p
â = Gasdruck (Pa)
t
â = Temperatur (°C)
Ï
â = Dichte (kg/mÂł)
M
â = Molare Masse (kg/mol)
K
â = Kompressionsmoduls (Pa)
c
log = Longitudinale Schallgeschwindigkeit (m/s)
c
trans = Transversale Schallgeschwindigkeit (m/s)
E
â = ElastizitĂ€tsmodul (N/mÂČ) (°C)
Μ
â = Poissonzahl (-)
Schallgeschwindigkeit verschiedener Stoffe
nach oben
EinfĂŒgungsdĂ€mmmaĂ eines SchalldĂ€mpfers
Das EinfĂŒgungsdĂ€mmmaĂ De ist die durch Vergleichsmessung mit und ohne SchalldĂ€mpfer ermittelte Pegelminderung.
D e = EinfĂŒgungsdĂ€mmmaĂ (dB)
L po = Schalldruckpegel ohne SchalldÀmpfer (dB)
L pm = Schalldruckpegel mit SchalldÀmpfer (dB)
D e = EinfĂŒgungsdĂ€mmmaĂ (dB)
L po = Schalldruckpegel ohne SchalldÀmpfer (dB)
L pm = Schalldruckpegel mit SchalldÀmpfer (dB)
nach oben
Beurteilungspegel
Der Beurteilungspegel ist auf einen Bezugszeitraum (z.B. Tag oder Nacht) umgerechneter mittlerer Schallpegel, bei dem durch
Pegelkorrekturen einzelne Besonderheiten der GerĂ€usche (Tonhaltigkeit, Impulshaltigkeit) zusĂ€tzlich berĂŒcksichtigt werden können. Treten
wĂ€hrend einer Beurteilungszeit unterschiedliche Emissionen auf oder sind unterschiedliche ZuschlĂ€ge fĂŒr Ton- und Impulshaltigkeit oder
Tageszeiten mit erhöhter Empfindlichkeit erforderlich, so ist zur Ermittlung der GerÀuschimmission wÀhrend der gesamten Beurteilungszeit
diese in geeigneter Weise in Teilzeiten T j aufzuteilen, in denen die Emissionen im Wesentlichen gleichartig und die ZuschlÀge konstant
sind. Der Beurteilungspegel wird fĂŒr die Beurteilungszeiten tags und nachts getrennt ermittelt.
L r = Beurteilungspegel (dB)
T r = tags 16 Std. nachts 8 oder 1 Std.
T j = Teilzeit j (Std.)
N = Anzahl der gewÀhlten Teilzeiten
L Aeq,j = Mittelungspegel wÀhrend der Teilzeit Tj (dB)
C met = meteorologische Korrektur (dB)
K T,j = Zuschlag fĂŒr Ton- und Informationshaltigkeit in der Teilzeit Tj (dB)
K I,j = Zuschlag fĂŒr Impulshaltigkeit in der Teilzeit Tj (dB)
K R,j = Zuschlag fĂŒr Tageszeiten mit erhöhter Empfindlichkeit in der Teilzeit Tj (dB)
nach oben
Strömungsrauschen
Strömungsrauschen in LuftkanÀlen nach VDI 2081
Bei der Durchströmung von Luft in Rohrleitungen treten StrömungsgerÀusche auf, die AbhÀngig sind von der Strömungsgeschwindigkeit, von
dem Querschnitt des Kanals und dem Turbulenzgrad. Die nachfolgenden Formeln können nur als NÀherungswerte angesehen werden, da
fertigungstechnische EinflĂŒsse einen groĂen Einfluss auf das Strömungsrauschen nehmen.
Das Strömungsrauschen sollte ca. 10 dB niedriger liegen als der Hauptschallpegel, da andernfalls sich der Hauptschallpegel
erhöht.
In der Literatur werden unterschiedliche Formeln fĂŒr das Strömungsrauschen genannt die nachfolgend aufgefĂŒhrt werden.
L w = Schallleistungspegel Strömungsrauschen (dB)
v = Strömungsgeschwindigkeit (m/s)
A = Rohrquerschnitt (mÂČ)
L w = Schallleistungspegel Strömungsrauschen (dB)
v = Strömungsgeschwindigkeit (m/s)
A = Rohrquerschnitt (mÂČ)
nach oben
Strömungsrauschen in Abgasleitungen
L w = Schallleistungspegel Strömungsrauschen (dB)
v = Strömungsgeschwindigkeit (m/s)
A = Rohrquerschnitt (mÂČ)
L w = Schallleistungspegel Strömungsrauschen (dB)
v = Strömungsgeschwindigkeit (m/s)
A = Rohrquerschnitt (mÂČ)
nach oben
Ănderung des Strömungsrauschens bei Ănderung des Volumenstroms
Î L w = Ănderung Schallleistungspegel Strömungsrauschen (dB)
V 1 = Ausgangs Volumenstrom (mÂł/s)
V 2 = geÀnderter Volumenstrom (m³/s)
Î L w = Ănderung Schallleistungspegel Strömungsrauschen (dB)
V 1 = Ausgangs Volumenstrom (mÂł/s)
V 2 = geÀnderter Volumenstrom (m³/s)
nach oben
VolumenstromÀnderung der Luft bei TemperaturÀnderung
ΠV = VolumenstromÀnderung der Luft (m³/s)
V 0 = Ausgangs Volumenstrom (mÂł/s)
T 1 = Ausgangs Temperatur (K)
T 2 = geÀnderte Temperatur (K)
ΠV = VolumenstromÀnderung der Luft (m³/s)
V 0 = Ausgangs Volumenstrom (mÂł/s)
T 1 = Ausgangs Temperatur (K)
T 2 = geÀnderte Temperatur (K)
nach oben
Oktavspektrum des Strömungsrauschens in Leitungen
Die Verteilung der Schallleistungspegel ĂŒber die Oktavfrequenzen kann NĂ€herungsweise nach folgendem Diagramm bestimmt werden. Dort
sind auf der Abszisse, aus Oktav-Mittenfrequenz und Strömungsgeschwindigkeit, die jeweiligen Korrekturwerte aufgetragen. Diese sind zum
oben ermittelten Gesamt-Schallleistungspegel zu addieren. Diese Zuordnung ist als NĂ€herungswert zu betrachten.

L w Okt = Oktav-Schallleistungspegel Strömungsrauschen (dB)
L w = Schallleistungspegel Strömungsrauschen (dB) â Gesamtwert s. oben
ÎL w = Korrekturwert fĂŒr Oktav-Schallleistungspegel (dB)
L w Okt = Oktav-Schallleistungspegel Strömungsrauschen (dB)
L w = Schallleistungspegel Strömungsrauschen (dB) â Gesamtwert s. oben
ÎL w = Korrekturwert fĂŒr Oktav-Schallleistungspegel (dB)
nach oben
Gesamtschallpegel
Berechnung des mittleren Gesamtschallpegels, aus den einzelnen Schallpegelwerten der einzelnen Frequenzen.
L pg = Gesamtschalldruckpegel (dB)
L p = Schalldruckpegel der einzelnen Frequenzen (dB)
n = Anzahl der Frequenzen
L pg = Gesamtschalldruckpegel (dB)
L p = Schalldruckpegel der einzelnen Frequenzen (dB)
n = Anzahl der Frequenzen
nach oben
nach oben
Bewertungsfaktoren von Schallpegeln
Um die LautstĂ€rkeempfindlichkeit des Menschen zu berĂŒcksichtigen, werden die Messwerte bei den einzelnen Frequenzen mit
Bewertungsfaktoren beaufschlagt. Diese Werte entsprechen dem Empfinden des menschlichen Gehörs.
Die wichtigsten Bewertungsfaktoren sind die sogenannten A-Frequenzbewertungsfaktoren.
L pA = Schalldruck mit Bewertung (dB(A))
L p = Schalldruckpegel ohne Bewertung (dB)
BF = Bewertungsfaktor (dB)
L pA = Schalldruck mit Bewertung (dB(A))
L p = Schalldruckpegel ohne Bewertung (dB)
BF = Bewertungsfaktor (dB)
Bewertungsfaktoren bei den einzelnen Frequenzen:
| Frequenz (Hz) |
31,5 |
63 |
125 |
250 |
500 |
1000 |
2000 |
4000 |
8000 |
16000 |
| A - Bewertung (dB) |
-39,52 |
-26,21 |
-16,18 |
-8,67 |
-3,25 |
0,00 |
1,20 |
0,96 |
-1,15 |
-6,71 |
| B - Bewertung (dB) |
-17,12 |
-9,36 |
-4,23 |
-1,36 |
-0,28 |
0,00 |
-0,09 |
-0,72 |
-2,94 |
-8,53 |
| C - Bewertung (dB) |
-3,03 |
-0,82 |
-0,17 |
0,00 |
0,03 |
0,00 |
-0,17 |
-0,83 |
-3,05 |
-8,64 |
nach oben
Berechnung der Bewertungskurven A, B und C von Schallpegeln in AbhÀngigkeit der Frequenz
Um der Tatsache Rechnung zu tragen, dass das menschliche Ohr Töne mit gleichem Schalldruck in unterschiedlichen Tonhöhen
unterschiedlich laut empfindet, werden so genannte Frequenzbewertungskurven verwendet.
Da die KrĂŒmmung der Kurven gleicher LautstĂ€rkepegel und damit der Frequenzgang des Gehörs vom Schalldruckpegel abhĂ€ngig ist, wurden fĂŒr
unterschiedlich hohe Schalldruckpegel unterschiedliche Bewertungskurven definiert:
A-Bewertung: Entspricht den Kurven gleicher LautstÀrkepegel bei ca. 20-40 phon
B-Bewertung: Entspricht den Kurven gleicher LautstÀrkepegel bei ca. 50-70 phon
C-Bewertung: Entspricht den Kurven gleicher LautstÀrkepegel bei ca. 80-90 phon
Bewertete Pegel werden durch den entsprechenden Buchstaben der Frequenzbewertung als Index der MessgröĂe gekennzeichnet.
A (f) = A-Bewertungsfaktor (dB)
B (f) = B-Bewertungsfaktor (dB)
C (f) = C-Bewertungsfaktor (dB)
f = Frequenz (Hz)
nach oben
Oktav- und Terzbandfrequenzen
Bei der Breite der FrequenzbÀnder verhÀlt sich die obere Grenzfrequenz des Spektrums zur unteren Grenzfrequenz wie folgt:
f o = obere Grenzfrequenz (Hz)
f u = untere Grenzfrequenz (Hz)
f o = obere Grenzfrequenz (Hz)
f u = untere Grenzfrequenz (Hz)
Frequenzwerte fĂŒr Terz- und Oktavband:
| Oktave |
|
31,5 |
|
|
63 |
|
|
125 |
|
|
250 |
|
| Terz |
25 |
31,5 |
40 |
50 |
63 |
80 |
100 |
125 |
160 |
200 |
250 |
315 |
| Oktave |
|
500 |
|
|
1000 |
|
|
2000 |
|
|
4000 |
|
| Terz |
400 |
500 |
630 |
800 |
1000 |
1250 |
1600 |
2000 |
2500 |
3150 |
4000 |
5000 |
| Oktave |
|
8000 |
|
|
16000 |
|
|
| Terz |
6300 |
8000 |
10000 |
12500 |
16000 |
20000 |
|
nach oben
Umrechnung von Terz- in Oktavspektren
Der Schalldruckpegel fĂŒr das Oktavspektrum ist aus dem Pegel auf der Oktavfrequenz und dem links und rechts liegenden Pegel der
Terzfrequenz zu ermitteln.
Eine Berechnung von Oktav- in Terzwerte ist nicht möglich.
L okt = Schalldruckpegel Oktavspektrum (dB)
L Terz = Schalldruckpegel Terzspektrum (dB)
L okt = Schalldruckpegel Oktavspektrum (dB)
L Terz = Schalldruckpegel Terzspektrum (dB)
nach oben




















































