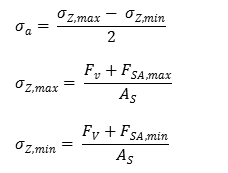Schraubenverbindung

Schraubenverbindung

Um Schraubenverbindungen rechnerisch und konstruktiv sicher auslegen zu können, müssen die Kräfte und Verformungen an Schrauben und verspannten Teilen sorgfältig untersucht werden.
Man unterscheidet Axialkraft und Querkraft belastete Schraubenverbindungen (exzentrisch belastete Schraubenverbindungen werden hier nicht behandelt).

Berechnungsgang

- Berechnung der Betriebskraft bzw. der Klemmkraft.

• Aus der Klemmkraft, Setzkraft und Betriebskraft wird die Vorspannkraft errechnet.
• Festlegung des Schraubendurchmessers aus der Vorspannkraft.
• Berechnung der Nachgiebigkeit der Schraube und der verspannten Teile.
• Berechnung des Kräfteverhältnisses und Festlegung des Krafteinleitungsfaktors.
• Berechnung der Vergleichsspannung und der Ausschlagsspannung und mit den zul. Werten vergleichen.
• Wenn die zul. Werte überschritten werden, den Schraubendurchmesser erhöhen und die Berechnung ab der Nachgiebigkeit der Teile neu durchführen.

Berechnungsprogramm für Axial- und Querkraft belastet Schraubenverbindung

Mit dem Berechnungsprogramm kann eine bestehende Schraubenverbindung berechnet werden (Gewindedurchmesser ist bekannt).

Berechnungsprogramm

Berechnungsprogramm zur Bestimmung des Schraubendurchmessers.

Das Berechnungsprogramm ermittelt überschlägig den Schraubendurchmesser auf Grund der gegebenen Belastungen.
Bei der Berechnung des Gewindedurchmessers werden verschiede Eingabewerte mit den folgenden Werten vorbelegt.
Nach der ersten Berechnung des Gewindedurchmessers können diese vorbelegten Werte nachträglich geändert werden.

Berechnungsprogramm

Gewindenennwerte

Gewindeabmessungen Metrisches ISO Gewinde

Gewindeabmessungen in Abhängigkeit vom Gewindenenndurchmesser und der Steigung für metrische ISO Gewinde. Abmessungen in mm.

Nenndurchmesser	D = d
Steigung	P
Gewindetiefe des Bolzengewindes	h3 = 0,6134 * P = H * 17 / 24
Gewindetiefe des Muttergewindes	H1 = 0,5413 * P
Rundung	R = 0,1443 * P
Flankendurchmesser	d2 = D2 = d - 0,6495 * P
Kerndurchmesser des Bolzengewindes	d3 = d - 1,22687 * P
Kerndurchmesser des Muttergewindes	D1 = d - 1,0825 * P
Flankenwinkel	60°
Steigungswinkel	φ = arctan[ P / (d2 * π)]
Spannungsquerschnitt	As = (d2 + d3)2 * π / 16
Spannungsdurchmesser	ds = (d2 + d3) / 2
Spannungsdurchmesser	ds = (As * 4 / π )0,5

Gewindeabmessungen Whitworth Regelgewinde BSW

Das Whitworth Regelgewinde unterscheidet sich gegenüber dem Metrischen ISO Gewinde hauptsächlich durch den Flankenwinkel von 55°.

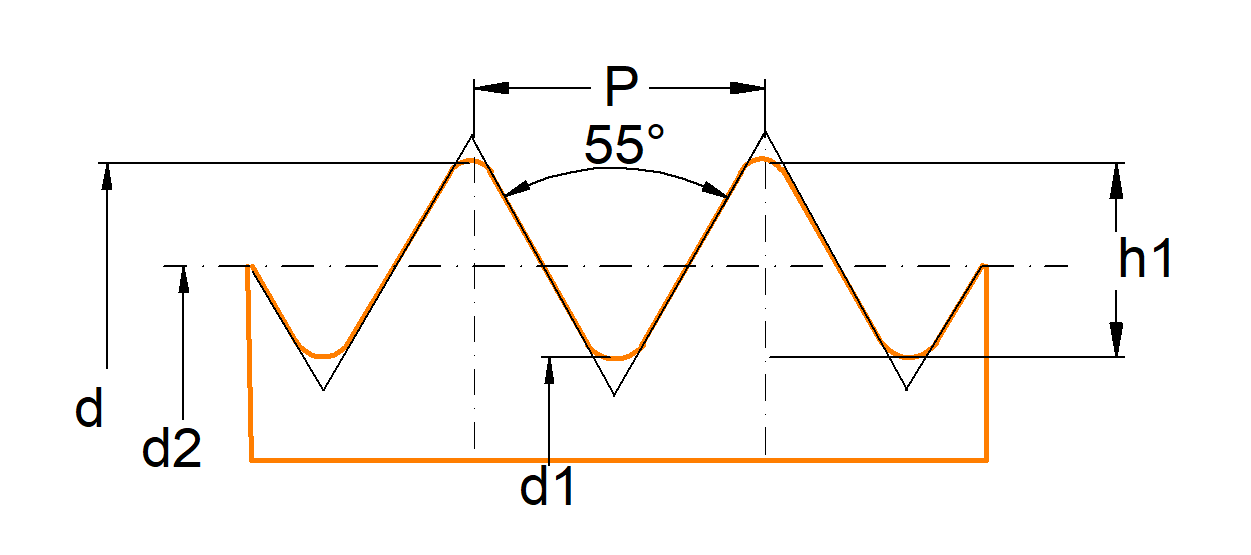
Nenndurchmesser	d
Gangzahl je inch	Z
Steigung	P = 2,54 / Z
Gewindetiefe	h1 = 0,64 * P
Flankendurchmesser	d2 = d - 0,6495 * P
Kerndurchmesser	d1 = d - 1,28 * P
Flankenwinkel	55°
Spannungsquerschnitt	As = (d2 + d3)2 * π / 16

Steigungswinkel

Der Steigungswinkel besagt, wie weit das Gewinde pro 360° Drehung steigt. Ein Regelgewinde hat einen mittleren Steigungswinkel von ca. 3°.

φ = Steigungswinkel (Grad)
P = Gewindesteigung (mm)
d ₂ = Flankendurchmesser (mm)

φ = Steigungswinkel (Grad)
P = Gewindesteigung (mm)
d ₂ = Flankendurchmesser (mm)

Gewindereibwinkel

Der Tangens des Reibungswinkels ist das Verhältnis von Reibungskraft zu Normalkraft in der Reibungsfläche, mit denen der Körper im Grenzzustand des Gleichgewichts belastet ist.
Er gibt die Neigung der resultierenden Kraft in der Reibungsfläche an.

ρ'   = Gewindereibwinkel (Grad)
μ_G = Gewindereibwert (-)
β   = Flankenwinkel (Grad)

ρ'   = Gewindereibwinkel (Grad)
μ_G = Gewindereibwert (-)
β   = Flankenwinkel (Grad)

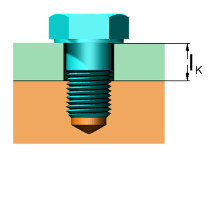
Klemmlänge

 Die Klemmlänge l_K ist die freie Länge einer Schraube, die unter Spannung gedehnt wird; das bedeutet:

• In einer Durchgangsbohrung der Abstand zwischen dem Schraubenkopf und der Mutter.
• In einer Sackbohrung oder bei einer Stiftschraube der Abstand zwischen dem Kopf (Mutter) und dem ersten Gewindegang, der in die Gewindebohrung eingreift.

Nachgiebigkeit der Schraube

Gesamtnachgiebigkeit der Schraube

Durch das Anziehen der Schraubenverbindung wird die Schraube gedehnt und die verschraubten Bauteile gestaucht.
Die Nachgiebigkeit der Schraube und Bauteile hat einen Einfluss auf die Verteilung der Betriebskraft auf die die einzelnen Teile.
Die Schraubennachgiebigkeit wird ermittelt, in dem die Schraube in verschiedene Einzelelemente aufgeteilt wird. Die einzelnen Schrauben Nachgiebigkeiten werden als in Reihe geschaltete Steifigkeiten berechnet.

δ _S = elastische Nachgiebigkeit gesamte Schraube (mm/N)
δ _K = elastische Nachgiebigkeit Schraubenkopf (mm/N)
δ _s,i = elastische Nachgiebigkeit Schraubenschaft (mm/N)
δ _fG = elastische Nachgiebigkeit freies Gewinde (mm/N)
δ _GM = elastische Nachgiebigkeit Mutter- bzw. Flanschgewindegänge (mm/N)

δ _S = elastische Nachgiebigkeit gesamte Schraube (mm/N)
δ _K = elastische Nachgiebigkeit Schraubenkopf (mm/N)
δ _s,i = elastische Nachgiebigkeit Schraubenschaft (mm/N)
δ _fG = elastische Nachgiebigkeit freies Gewinde (mm/N)
δ _GM = elastische Nachgiebigkeit Mutter- bzw. Flanschgewindegänge (mm/N)

Schraubenkopf

Für den Schraubenkopf wird eine Ersatzdehnlänge von 0,4*d angesetzt.

δ _K = elastische Nachgiebigkeit Schraubenkopf (mm/N)
l _K = Ersatzdehnlänge Schraubenkopf (mm)
E _S = E-Modul Schraube (N/mm2)
A _N = Nennquerschnittsfläche Schraube (mm²)
d = Schraubennenndurchmesser (mm)

δ _K = elastische Nachgiebigkeit Schraubenkopf (mm/N)
l _K = Ersatzdehnlänge Schraubenkopf (mm)
E _S = E-Modul Schraube (N/mm2)
A _N = Nennquerschnittsfläche Schraube (mm²)
d = Schraubennenndurchmesser (mm)

Schraubenschaft

Für den Schraubenschaft (Abschnitt ohne Gewinde) wird die Schraubensteifigkeit auf den Schaftdurchmesser bezogen.

δ _s,i = elastische Nachgiebigkeit Schraubenschaft (mm/N)
l _s,i = Schaftlänge (mm)
E _S = E-Modul Schraube (N/mm2)
A _s,i = Nennquerschnittsfläche Schraubenschaft (mm²)
d _i = Schraubenschaft-Durchmesser (mm)

δ _s,i = elastische Nachgiebigkeit Schraubenschaft (mm/N)
l _s,i = Schaftlänge (mm)
E _S = E-Modul Schraube (N/mm2)
A _s,i = Nennquerschnittsfläche Schraubenschaft (mm²)
d _i = Schraubenschaft-Durchmesser (mm)

Freies Gewinde

Beim freien Gewinde, welches nicht mit einem Muttergewinde verbunden ist, wird die Schraubensteifigkeit auf den Spannungsquerschnitt des Gewindes bezogen

δ _fG = elastische Nachgiebigkeit freies Gewinde (mm/N)
l _fG = Länge freies Gewinde (mm)
E _S = E-Modul Schraube (N/mm2)
A _S = Spannungsquerschnitt (mm²)

δ _fG = elastische Nachgiebigkeit freies Gewinde (mm/N)
l _fG = Länge freies Gewinde (mm)
E _S = E-Modul Schraube (N/mm2)
A _S = Spannungsquerschnitt (mm²)

Schraubenverbindungsart - Durchsteckverbindung - Einschraubverbindung

Bei dem Gewindeanteil welches mit dem Muttergewinde verbunden ist, wird je nach Verbindungsart die Dehnlänge wie folgt festgelegt:
- Durchsteckverbindung (Schraube mit Mutter) - l_G = 0,4 * d
- Einschraubverbindung (Schraube in Befestigungsplatte verschraubt) - l_G = 0,33 * d

Durchsteckverbindung

δ _GM = elastische Nachgiebigkeit Mutter (mm/N)
l _G = 0,4 * d (mm)
E _S = E-Modul Mutter (N/mm2)
A _N = Nennquerschnitt (mm²) - Flankendurchmesser

δ _GM = elastische Nachgiebigkeit Mutter (mm/N)
l _G = 0,4 * d (mm)
E _S = E-Modul Mutter (N/mm2)
A _N = Nennquerschnitt (mm²) - Flankendurchmesser

Einschraubverbindung

δ _GM = elastische Nachgiebigkeit eingeschraubtes Gewinde (mm/N)
l _G = 0,33 * d (mm)
E _P = E-Modul Innengewinde Flansch (N/mm2)
A _N = Nennquerschnitt (mm²) - Flankendurchmesser

δ _GM = elastische Nachgiebigkeit eingeschraubtes Gewinde (mm/N)
l _G = 0,33 * d (mm)
E _P = E-Modul Innengewinde Flansch (N/mm2)
A _N = Nennquerschnitt (mm²) - Flankendurchmesser

Einzelsteifigkeiten einer Schraube.

Nachgiebigkeit der verspannten Teile

Gesamtnachgiebigkeit verspannte Teile

Bei den verspannten Teilen, breitet sich über die Klemmlänge eine tonnenförmige Druckspannung aus. Die Schwierigkeit liegt in der Ermittlung eines Ersatzquerschnitts, da die auf Druck beanspruchten Zonen keinen Zylinder bilden. In den folgenden Formeln wird der Ersatzquerschnitt für einen Zylinder ermittelt, der die Abhängigkeit der seitlichen Ränder berücksichtigt.

δ _P = elastische Nachgiebigkeit der verspannten Teile (mm/N)
l _K = Klemmlänge (mm)
E _P = E-Modul verspannte Teile (N/mm2)
A _ers = Ersatzquerschnitt (mm²)

δ _P = elastische Nachgiebigkeit der verspannten Teile (mm/N)
l _K = Klemmlänge (mm)
E _P = E-Modul verspannte Teile (N/mm2)
A _ers = Ersatzquerschnitt (mm²)

Ersatzquerschnitt [4]

Der Ersatzquerschnitt ist gültig für die Durchsteck- wie für die Einschraubverbindung.

Ausführung 1 - Hülsenausführung

---

Ausführung 2 - Druckkegel wird durch Flanschkante oder benachbarte Schraube eingegrenzt

---

Ausführung 3 - Druckkegel wird nicht eingegrenzt

---

D _a = Durchmesser Druckkegel (mm)
d _K = Außendurchmesser Schraubenkopf (mm)
A _ers = Ersatzquerschnitt (mm²)
d _i = Bohrungsdurchmesser (mm)
l _K = Klemmlänge (mm)

Klemmkraft

Klemmkraft bei Axialkraftbelastung

Für die Bestimmung der min. Restklemmkraft bei Axialbelastung, können folgende Faktoren angenommen werden.

Fk = Klemmkraft
FB = Axialkraft (Betriebskraft)

Klemmkraft zur Übertragung einer Querkraft durch Reibschluss

Bei Querkraftbelastung einer Schraubenverbindung ist für die Klemmkraft hauptsächlich der Reibwert in der Trennfuge maßgebend.

F _K,Q = erf. Klemmkraft bei Querkraftbelastung (N)
F _Q = Querkraft (N)
S _R = Rutschsicherheit (-)
μ _T = Haftreibwert Trennfuge (-)
i = Anzahl Trennfugen (-)
n = Anzahl Schrauben (-)

F _K,Q = erf. Klemmkraft bei Querkraftbelastung (N)
F _Q = Querkraft (N)
S _R = Rutschsicherheit (-)
μ _T = Haftreibwert Trennfuge (-)
i = Anzahl Trennfugen (-)
n = Anzahl Schrauben (-)

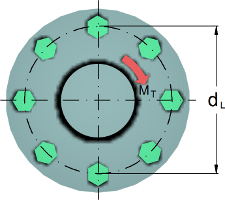
Klemmkraft bei einem Flansch zur Übertragung eines Drehmoments

Eine sichere Flanschverbindung wird durch den Reibwert und die Anzahl der Schrauben sowie dem Lochkreisdurchmesser bestimmt.

F _K,erf = erf. Klemmkraft bei Drehmomentbelastung (N)
M   = Drehmoment (Nmm)
n   = Anzahl Schrauben (-)
μ _T = Haftreibwert Trennfuge (-)
d _L = Lochkreisdurchmesser (mm)

F _K,erf = erf. Klemmkraft bei Drehmomentbelastung (N)
M   = Drehmoment (Nmm)
n   = Anzahl Schrauben (-)
μ _T = Haftreibwert Trennfuge (-)
d _L = Lochkreisdurchmesser (mm)

Schraubenkraft und -größe einer Flanschverbindung mit Dichtung

Die Berechnung von Schrauben an Flanschverbindungen mit Dichtungen, finden Sie hier.
Die Berechnung erfolgt nach AD 2000 Merkblatt B7 - Schrauben.

Schraubenabstand bei Dichtflächen [3]

Bei druckbeaufschlagten Abschlussdeckeln kann der Schraubenabstand nach folgender Formel festgelegt werden, um die Dichtigkeit zu gewährleisten.

l   = Schraubenabstand (mm)
d   = Durchmesser Durchgangsloch (mm)

l   = Schraubenabstand (mm)
d   = Durchmesser Durchgangsloch (mm)

Konsolenverschraubungen

Schraubenkraft einer Konsolenverschraubung bei einer Biegemomentbelastung

Durch die außenliegende Kraft, wirkt in der Flanschfläche eine Querkraft und ein Moment.
Die Querkraft ist durch Reibschluss aufzunehmen.
Das Moment wird über die Schraubenaxialkräfte aufgenommen, hierbei wird von einer linearen Verteilung der Schraubenkräfte ausgegangen.
Als Kippkante für die Schraubenkräfte, wird im gezeichneten Beispiel, die untere Schraubenreihe angenommen. Je nach Flanschsteifigkeit ist die Lage der Kippkante festzulegen.

Axialkraft einer Schraube mit Abstand Ly

Klemmkraft für Reibschlussverbindung

Gesamte Schraubenkraft

F _a,Ly = Schraubenaxialkraft (N)
F   = Belastung (N)
L _x = Abstand Belastung zur Flanschfläche (mm)
L _y = Abstand von der zu berechnenden Schraubenkraft
        bis zur Kippkante (mm) 
n _i = Anzahl Schrauben mit Abstand Li (mm)
L _i = Schraubenabstand von der Kippkante (mm)
F _K,Q = Klemmkraft je Schraube (N)
μ _T = Reibwert in der Flanschfläche (-)
n   = Schraubenanzahl gesamt (-)

F _a,Ly = Schraubenaxialkraft (N)
F   = Belastung (N)
L _x = Abstand Belastung zur Flanschfläche (mm)
L _y = Abstand von der zu berechnenden Schraubenkraft
        bis zur Kippkante (mm) 
n _i = Anzahl Schrauben mit Abstand Li (mm)
L _i = Schraubenabstand von der Kippkante (mm)
F _K,Q = Klemmkraft je Schraube (N)
μ _T = Reibwert in der Flanschfläche (-)
n   = Schraubenanzahl gesamt (-)

Berechnungsprogramm Schraubenbelastung an einer Konsolenverschraubung bei Biegebelastung

In Abhängigkeit der Steifigkeit der Konsolenplatte kann die Kippkante festgelegt werden.

Berechnungsprogramm

Schrauben-Querkraftbelastung einer Konsolenverschraubung bei Torsionsbelastung

Durch das Torsionsmoment wirkt an der Schraube eine Querkraft.
Bei der Berechnung wird angenommen, dass das Torsionsmoment im Schwerpunkt der Schraubenanordnung wirkt.
Die horizontale und vertikale Belastung wird gleichmäßig auf die Schrauben aufgeteilt.

Torsionsmoment

Polares Trägheitsmoment der Schraubenanordnung

Schraubenkräfte

M _z = Torsionsmoment (Nmm)
F _H = Horizontale Belastung (N)
F _V = Vertikale Belastung (N)
l _x = horizontaler Abstand von F_V (mm)
l _y = vertikaler Abstand von F_H (mm)
I_ps = polares Trägheitsmoment der Schraubenanordnung (mm²)
X _S,i = Schraubenabstand in X-Richtung zum Schwerpunkt (mm)
Y _S,i = Schraubenabstand in Y-Richtung zum Schwerpunkt (mm)
F _S,x = Schraubenkraft in Richtung x (N)
F _S,y = Schraubenkraft in Richtung y (N)
F _S,res = Resultierende Schraubenkraft (N)
n _S = Anzahl Schrauben (-)

M _z = Torsionsmoment (Nmm)
F _H = Horizontale Belastung (N)
F _V = Vertikale Belastung (N)
l _x = horizontaler Abstand von F_V (mm)
l _y = vertikaler Abstand von F_H (mm)
I_ps = polares Trägheitsmoment der Schraubenanordnung (mm²)
X _S,i = Schraubenabstand in X-Richtung zum Schwerpunkt (mm)
Y _S,i = Schraubenabstand in Y-Richtung zum Schwerpunkt (mm)
F _S,x = Schraubenkraft in Richtung x (N)
F _S,y = Schraubenkraft in Richtung y (N)
F _S,res = Resultierende Schraubenkraft (N)
n _S = Anzahl Schrauben (-)

Berechnungsprogramm Schrauben-Querkraftbelastung an einer Konsolenverschraubung bei Torsionsbelastung

Es wird angenommen, dass sich die Konsole um den Schwerpunkt der Schraubenverbindung dreht.
Die horizontale und vertikale Belastung wird gleichmäßig auf die Schrauben aufgeteilt.

Berechnungsprogramm

Vorauswahl Gewindedurchmesser

Tabelle Vorspannkraft

Nach Berechnung der Vorspannkraft über die Klemm- und Betriebskraft und den Anziehfaktor, kann aus Tabellen in denen die Vorspannkraft in Abhängigkeit vom Schraubendurchmesser und der Festigkeitsklasse aufgeführt ist, der entsprechende Schraubendurchmesser festgelegt werden.
Forderung: Fv Tabelle > Fv Rechnung

Erforderlicher Spannungsquerschnitt - Näherungsformel

Beim Anziehen wird die Schraube durch die Vorspannkraft auf Zug, durch das Gewindereibmoment auf Torsion beansprucht. Beide Größen können erst später berechnet werden. Aus diesem Grund wird zunächst reine Zugspannung angenommen, hervorgerufen durch die Schraubenkraft (F S = F K + F A).
Auf Grund der nicht berücksichtigten Torsionsspannung wird die zul. Spannung nur ca. 0,6 ... 0,8 * R _p0,2 angesetzt. Unter Berücksichtigung des Anziehfaktors alpha A wird der erforderliche Spannungsquerschnitt wie folgt berechnet:

A _S = Spannungsquerschnitt (mm²)
α _A = Anziehfaktor (-)
F _K = Klemmkraft (N)
F _A = Betriebskraft (N)
ν   = Ausnutzung Streckgrenze (-) - ca. 0,6...0,8
R _p0,2 = Streckgrenze (N/mm2)

A _S = Spannungsquerschnitt (mm²)
α _A = Anziehfaktor (-)
F _K = Klemmkraft (N)
F _A = Betriebskraft (N)
ν   = Ausnutzung Streckgrenze (-) - ca. 0,6...0,8
R _p0,2 = Streckgrenze (N/mm2)

Vorspannkraft

Mindest Vorspannkraft

Für eine sichere Schraubenverbindung ist eine mindest Vorspannkraft erforderlich, um ein klaffen der Befestigungsflansche zu verhindern.

F _V,min = Mindest Vorspannkraft (N)
F _Z = Setzkraft (N)
F _K = Klemmkraft (N)
n   = Krafteinleitungsfaktor (-)
Φ _K = Kraftverhältnis (-)
F _A = Axialkraft (N)

F _V,min = Mindest Vorspannkraft (N)
F _Z = Setzkraft (N)
F _K = Klemmkraft (N)
n   = Krafteinleitungsfaktor (-)
Φ _K = Kraftverhältnis (-)
F _A = Axialkraft (N)

Maximale Vorspannkraft

Die maximale Vorspannkraft ist gegenüber der min. Vorspannkraft um den Anziehfaktor α A größer. Der Anziehfaktor berücksichtigt die unterschiedlichen Ungenauigkeiten der verschiedenen Anziehverfahren. Um die gewünschte Vorspannkraft tatsächlich zu erreichen, wird die Vorspannkraft um den Anziehfaktor erhöht.

F _V = Maximale Vorspannkraft (N)
α _A = Anziehfaktor (-) siehe Tabelle unten
F _V,min = Mindest Vorspannkraft (N)

F _V = Maximale Vorspannkraft (N)
α _A = Anziehfaktor (-) siehe Tabelle unten
F _V,min = Mindest Vorspannkraft (N)

Anziehfaktoren

Die Anziehfaktoren berücksichtigen die unterschiedlichen Ungenauigkeiten der verschiedenen Anziehverfahren.

(* (α_A - 1) / (α_A + 1)   Auszug aus VDI 2230

Vorspannkraft bei zul. Spannung

Sind die Gewindeabmessungen bekannt, kann die Vorspannkraft aus der zulässigen Spannung berechnet werden.

F _V = Vorspannkraft (N)
σ _zul = zul. Spannung (N/mm2)
A _S = Spannungsquerschnitt (mm²)
d ₂ = Flankendurchmesser (mm)
φ°   = Steigungswinkel (Grad)
ρ'   = Gewindereibwinkel (Grad)
W _p = pol. Widerstandsmoment (mm³)
d _s = Spannungsdurchmesser aus A_s (mm)
A _s = Spannungsquerschnitt (mm²)
R _p0,2 = Streckgrenze Schraubenwerkstoff (N/mm²)
P = Gewindesteigung (mm)
d ₂ = Flankendurchmesser (mm)
μ _G = Gewindereibwert (-)
β = Flankenwinkel (Grad)
d _S = Spannungsdurchmesser (mm)

F _V = Vorspannkraft (N)
σ _zul = zul. Spannung (N/mm2)
A _S = Spannungsquerschnitt (mm²)
d ₂ = Flankendurchmesser (mm)
φ°   = Steigungswinkel (Grad)
ρ'   = Gewindereibwinkel (Grad)
W _p = pol. Widerstandsmoment (mm³)
d _s = Spannungsdurchmesser aus A_s (mm)
A _s = Spannungsquerschnitt (mm²)
R _p0,2 = Streckgrenze Schraubenwerkstoff (N/mm²)
P = Gewindesteigung (mm)
d ₂ = Flankendurchmesser (mm)
μ _G = Gewindereibwert (-)
β = Flankenwinkel (Grad)
d _S = Spannungsdurchmesser (mm)

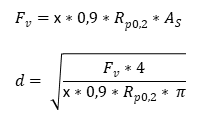
Näherungsformel für Vorspannkraft bzw. Schraubendurchmesser bei ca. 90 % der Streckgrenze

Diese Formel ist nur eine grobe Näherungsformel und ist nur für eine Überschlagsberechnung gültig.

F _V = Vorspannkraft (N)
R _p0,2 = Streckgrenze (N/mm²)
A _S = Spannungsquerschnitt (mm²)
d   = Schraubendurchmesser (mm)
x   = Faktor (-)
Faktor x in Abhängigkeit des Reibwertes:
x = 0,90 bei μ 0,08
x = 0,85 bei μ 0,10
x = 0,82 bei μ 0,12
x = 0,80 bei μ 0,14

F _V = Vorspannkraft (N)
R _p0,2 = Streckgrenze (N/mm²)
A _S = Spannungsquerschnitt (mm²)
d   = Schraubendurchmesser (mm) x   = Faktor (-)
Faktor x in Abhängigkeit des Reibwertes:
x = 0,90 bei μ 0,08
x = 0,85 bei μ 0,10
x = 0,82 bei μ 0,12
x = 0,80 bei μ 0,14

Vorspannkraft in der Schraubenverbindung bei erhöhter Temperatur

Die Tragfähigkeit von Schraubenverbindungen bei erhöhter Temperatur, kann durch Änderung folgender Einflüsse nachhaltig beeinträchtigt werden, Festigkeits- und Zähigkeitskennwerte, Elastizitätsmodul, Thermischer Ausdehnungskoeffizient und Wärmeleitfähigkeit.
Ein Abfall der Vorspannkraft bzw. eine Erhöhung durch Wärmedehnungen kann zum Versagen der Schraubenverbindung führen.
Bei unterschiedlichen Ausdehnungskoeffizienten ändert sich die Vorspannkraft wie folgt:

- Ausdehnungskoeffizient der Schraube und Platte ist gleich, die Vorspannkraft ändert sich nicht.

Vorspannkraft bei erhöhter Temperatur

Mit der vereinfachten Annahme l_S= l_P und α_S*ΔT_S sowie α_P*ΔT_P < 1 vereinfacht sich Formel zu

Wenn der E-Modul von Schraube und Platte bei Raum- und erhöhter Temperatur gleich angenommen werden kann, berechnet sich die Vorspannkraftdifferenz wie folgt:

---

F_v,RT = Vorspannkraft bei Raumtemperatur (N)
F _v,T = Vorspannkraft bei erhöhter Temperatur (N)
ΔF _v = Vorspannkraft-Differenz durch Temperaturdifferenz (N)
l _S = Schraubenlänge = Klemmlänge im unbelasteten Zustand (mm)
l _P = Plattenlänge = Klemmlänge im unbelasteten Zustand (mm)
A _S = Gewinde Nennspannungsquerschnitt (mm²)
A _P = Querschnitt der verspannten Teile (mm²)
E _S,RT = Elastizitätsmodul Schraube bei Raumtemperatur (N/mm²)
E _S,T = Elastizitätsmodul Schraube bei erhöhter Temperatur (N/mm²)
E _P,RT = Elastizitätsmodul Platte bei Raumtemperatur (N/mm²)
E _P,T = Elastizitätsmodul Platte bei erhöhter Temperatur (N/mm²)
α _S = Ausdehnungskoeffizient Schraube (1/K)
α _P = Ausdehnungskoeffizient Platte (1/K)
ΔT _S = Temperaturdifferenz Schraube (°C)
ΔT _P = Temperaturdifferenz Platte (°C)

Mindeststreckgrenze bei erhöhter Temperatur

Bei Schraubenverbindungen die einer erhöhten Temperatur ausgesetzt sind, ist die geringere Streckgrenze zu berücksichtigen.

Anhaltswerte für den Elastizitätsmodul bei erhöhter Temperatur

Tabelle mit dem Elastizitätsmodul bei erhöhter Temperatur.

Anhaltswerte für den Wärmeausdehnungskoeffizienten bei erhöhter Temperatur

Tabelle mit den Werten des Wärmeausdehnungskoeffizienten bei erhöhter Temperatur.

Auszug aus DIN EN 10269

Kräfte in der Schraubenverbindung

Kräfteverhältnis

Das Kräfteverhältnis Φ_K ist der Quotient aus der Schraubenzusatzkraft F _SA und der axialen Betriebskraftkomponente F _A

Φ _K = Kraftverhältnis (-)
δ _P = elastische Nachgiebigkeit der verspannten Teile (mm/N)
δ _S = elastische Nachgiebigkeit der Schraube (mm/N)
F _SA = Schraubenzusatzkraft (N)
F _A = axiale Betriebskraft (N)

Φ _K = Kraftverhältnis (-)
δ _P = elastische Nachgiebigkeit der verspannten Teile (mm/N)
δ _S = elastische Nachgiebigkeit der Schraube (mm/N)
F _SA = Schraubenzusatzkraft (N)
F _A = axiale Betriebskraft (N)

Krafteinleitungsfaktor

Der Krafteinleitungsfaktor n berücksichtigt die örtliche Einleitung der Betriebskraft in die verspannten Teile.
Je nach Krafteinleitungsort wird ein Teil der verspannten Teile entlastet und der andere Teil gestaucht. Hiermit ändert sich die Steifigkeit der verspannten Teile, sowie die federnde Länge der Schraube. Diese Steifigkeitsänderung wird durch den Krafteinleitungsfaktor berücksichtigt.
Bei nicht genauer Kenntnis der Krafteinleitung ist n=0,5 anzunehmen.
Bei Querkraft beanspruchten Schraubenverbindungen, die über Reibschluß die Kräfte übertragen, ist der Krafteinleitungsfaktor n = 0.

nach oben

Vorspannungsänderung durch Setzung [5]

Durch die Rauigkeit der Oberflächen treten Setzungen auf. Um diesen Setzbetrag wird die Vorspannkraft vermindert.

Setzbetrag und Vorspannkraftverlust bei Starrschrauben

Setzbetrag unter Berücksichtigung der Schraubennachgiebigkeit bei Dehnschrauben

f _z = Setzbetrag (mm)
l _K = Klemmlänge (mm)
d   = Nenndurchmesser (mm)
F _Z = Vorspannkraftverlust durch Setzen (N)
Φ _K = Kraftverhältnis (-)
δ _P = elastische Nachgiebigkeit der verspannten Teile (mm/N)
δ _S = elastische Nachgiebigkeit der Schraube (mm/N)
E _S = E-Modul der Schraube (N/mm²)

f _z = Setzbetrag (mm)
l _K = Klemmlänge (mm)
d   = Nenndurchmesser (mm)
F _Z = Vorspannkraftverlust durch Setzen (N)
Φ _K = Kraftverhältnis (-)
δ _P = elastische Nachgiebigkeit der verspannten Teile (mm/N)
δ _S = elastische Nachgiebigkeit der Schraube (mm/N)
E _S = E-Modul der Schraube (N/mm²)

Richtwerte für Setzbeträge in Abhängigkeit der Rautiefe n. [VDI 2230]

Die Werte sind gültig für Stahl Flansche. Als Mittelwert kann 0,01 mm angenommen werden.

Empirische Formel für den Setzbetrag, abgeleitet aus der VDI Tabelle

Für die analytische Schraubenberechnung, wurde in [6] die folgende empirische Formel entwickelt, auf der Grundlage der VDI Tabelle mit den einzelnen Setzbeträgen.

n _KM = Anzahl der Kopf-/Mutterauflageflächen (-)
n _T = Anzahl inneren Trennfugen (-)
S   = Schubkoeffizient 0=Zug/Druckbelastung / 1=Schubbelastung
Rz _min = Rauheitsbereich

Rzmin	Einteilung VDI Tabelle
0 μm	< 10 μm
10 μm	10 μm bis 40 μm
40 μm	40 μm bis 160 μm

Betriebskraftanteil

Betriebskraftanteil auf die verspannten Teile

Der Betriebskraftanteil auf die verspannten Teile, ist der Betriebskraftanteil zwischen Klemmkraft und Vorspannkraft.

F _PA = Betriebskraftanteil auf die verspannten Teile (N)
n   = Krafteinleitungsfaktor (-)
Φ _K = Kraftverhältnis (-)
F _A = axiale Betriebskraft (N)

F _PA = Betriebskraftanteil auf die verspannten Teile (N)
n   = Krafteinleitungsfaktor (-)
Φ _K = Kraftverhältnis (-)
F _A = axiale Betriebskraft (N)

Betriebskraftanteil auf die Schraube

Der Betriebskraftanteil auf die Schraube, ist der Betriebskraftanteil zwischen Vorspannkraft und maximaler Schraubenkraft.

F _S,A = Betriebskraftanteil auf die Schraube (N)
n   = Krafteinleitungsfaktor (-)
Φ _K = Kraftverhältnis (-)
F _A = axiale Betriebskraft (N)

F _S,A = Betriebskraftanteil auf die Schraube (N)
n   = Krafteinleitungsfaktor (-)
Φ _K = Kraftverhältnis (-)
F _A = axiale Betriebskraft (N)

Maximale Schraubenkraft

Die maximale Schraubenkraft berechnet sich aus Vorspannkraft plus Betriebskraftanteil auf die Schraube.

F _S = Schraubenkraft (N)
F _V = Vorspannkraft (N)
n   = Krafteinleitungsfaktor (-)
Φ _K = Kraftverhältnis (-)
F _A = axiale Betriebskraft (N)

F _S = Schraubenkraft (N)
F _V = Vorspannkraft (N)
n   = Krafteinleitungsfaktor (-)
Φ _K = Kraftverhältnis (-)
F _A = axiale Betriebskraft (N)

Spannungen

Zugspannung

Die Zugspannung in einer Schraubenverbindung bezieht sich auf den Spannungsquerschnitt des Gewindes.
Bei Dehnschrauben ist der Querschnitt des Dehnschafts maßgebend.

σ _Z = Zugspannung (N)
F _S = Schraubenkraft (N)
A _S = Spannungsquerschnitt (mm²)

σ _Z = Zugspannung (N)
F _S = Schraubenkraft (N)
A _S = Spannungsquerschnitt (mm²)

Torsionsspannung

Durch die Reibung im Gewinde und unter der Kopfauflage wird die Schraube beim Anziehen auf Torsion beansprucht.

τ   = Torsionsspannung (N/mm2)
F _V = Vorspannkraft (N)
d ₂ = Flankendurchmesser (mm)
φ°   = Steigungswinkel (Grad)
ρ°   = Gewindereibwert (Grad)
W _P = pol. Widerstandsmoment (mm³)
d _s = Spannungsdurchmesser aus A_s (mm)
A _s = Spannungsquerschnitt (mm²)

τ   = Torsionsspannung (N/mm2)
F _V = Vorspannkraft (N)
d ₂ = Flankendurchmesser (mm)
φ°   = Steigungswinkel (Grad)
ρ°   = Gewindereibwert (Grad)
W _P = pol. Widerstandsmoment (mm³)
d _s = Spannungsdurchmesser aus A_s (mm)
A _s = Spannungsquerschnitt (mm²)

Vergleichsspannung

Die maßgebende Spannung für eine Schraubenverbindung, ist die Vergleichspannung nach der Gestaltänderungs-Hypothese.

σ _V = Vergleichsspannung (N/mm2)
σ _Z = Zugspannung (N/mm²)
τ   = Torsionsspannung (N/mm2)

σ _V = Vergleichsspannung (N/mm2)
σ _Z = Zugspannung (N/mm²)
τ   = Torsionsspannung (N/mm2)

Ausschlagsspannung bei dynamischer Betriebskraft

Bei dynamisch beanspruchten Schraubenverbindungen, ist die dynamische Betriebskraft maßgebend für die Haltbarkeit der Verbindung.

σ _a = Ausschlagsspannung (N/mm2)
σ _Z,max = max. Zugspannung (N/mm²)
σ _Z,min = min. Zugspannung (N/mm²)
F _V = Vorspannkraft (N)
F _SA,max = Axialkraftanteil auf die Schraube bei max. Betriebskraft (N)
F _SA,min = Axialkraftanteil auf die Schraube bei min. Betriebskraft (N)
A _S = Spannungsquerschnitt (mm²)

σ _a = Ausschlagsspannung (N/mm2)
σ _Z,max = max. Zugspannung (N/mm²)
σ _Z,min = min. Zugspannung (N/mm²)
F _V = Vorspannkraft (N)
F _SA,max = Axialkraftanteil auf die Schraube bei max. Betriebskraft (N)
F _SA,min = Axialkraftanteil auf die Schraube bei min. Betriebskraft (N)
A _S = Spannungsquerschnitt (mm²)

Näherungsformel für die zul. Ausschlagsspannung

Die zulässige Ausschlagspannung kann nach folgender Näherungsformel berechnet werden.

σ _a = Ausschlagsspannung (N/mm2)
d   = Nenndurchmesser (mm)
F _m = Mittelkraft der dyn. Betriebskraft (N)
F _0,2 = Schraubenkraft an der Streckgrenze (N)

σ _a = Ausschlagsspannung (N/mm2)
d   = Nenndurchmesser (mm)
F _m = Mittelkraft der dyn. Betriebskraft (N)
F _0,2 = Schraubenkraft an der Streckgrenze (N)

Anziehdrehmoment

Anziehdrehmoment berechnen

Um die Schraubenverbindung mit der zulässigen Vorspannkraft zu beanspruchen, ist die Schraube mit einem definierten Anziehdrehmoment anzuziehen.

M _A = Anziehdrehmoment (Nmm)
F _V = Vorspannkraft (N)
d ₂ = Flankendurchmesser (mm)
ρ'   = Gewindereibwert (Grad)
φ°   = Steigungswinkel (Grad)
P   = Gewindesteigung (mm)
μ _G = Reibwert Gewinde (-)
μ _K = Reibwert Kopfauflage (-)
β   = Flankenwinkel (Grad)
d _K,R = Reibdurchmesser Kopfauflage (mm)
d _K = Außendurchmesser Kopfauflage (mm)
d _i = Bohrungsdurchmesser (mm)

M _A = Anziehdrehmoment (Nmm)
F _V = Vorspannkraft (N)
d ₂ = Flankendurchmesser (mm)
ρ'   = Gewindereibwert (Grad)
φ°   = Steigungswinkel (Grad)
P   = Gewindesteigung (mm)
μ _G = Reibwert Gewinde (-)
μ _K = Reibwert Kopfauflage (-)
β   = Flankenwinkel (Grad)
d _K,R = Reibdurchmesser Kopfauflage (mm)
d _K = Außendurchmesser Kopfauflage (mm)
d _i = Bohrungsdurchmesser (mm)

Bei einem Flankenwinkel von 60° und gleichem Reibwert von Gewinde und Schraubenkopf vereinfacht sich die Formel zu:

M _A = Anziehdrehmoment (Nmm)
F _V = Vorspannkraft (N)
d ₂ = Flankendurchmesser (mm)
μ _ges = Reibwert für Gewinde und Kopfauflage (-)
d _K,R = Reibdurchmesser Kopfauflage (mm)
d _K = Außendurchmesser Kopfauflage (mm)
d _i = Bohrungsdurchmesser (mm)
d   = Nenndurchmesser (mm)

M _A = Anziehdrehmoment (Nmm)
F _V = Vorspannkraft (N)
d ₂ = Flankendurchmesser (mm)
μ _ges = Reibwert für Gewinde und Kopfauflage (-)
d _K,R = Reibdurchmesser Kopfauflage (mm)
d _K = Außendurchmesser Kopfauflage (mm)
d _i = Bohrungsdurchmesser (mm)
d   = Nenndurchmesser (mm)

Losdrehmoment

Beim Losreißmoment (Moment um die Schraube in Drehung zu versetzen) sind bei den Reibwerten die Haftreibwerte einzusetzen.

M _L = Losdrehmoment (Nmm)
F _V = Vorspannkraft (N)
d ₂ = Flankendurchmesser (mm)
ρ'   = Gewindereibwert (Grad)
φ°   = Steigungswinkel (Grad)
μ _K = Reibwert Kopfauflage (-)
d _K,R = Reibdurchmesser Kopfauflage (mm)
d _K = Außendurchmesser Kopfauflage (mm)
d _i = Bohrungsdurchmesser (mm)
P   = Gewindesteigung (mm)
μ _G = Gewindereibwert (-)
β   = Flankenwinkel (Grad)

M _L = Losdrehmoment (Nmm)
F _V = Vorspannkraft (N)
d ₂ = Flankendurchmesser (mm)
ρ'   = Gewindereibwert (Grad)
φ°   = Steigungswinkel (Grad)
μ _K = Reibwert Kopfauflage (-)
d _K,R = Reibdurchmesser Kopfauflage (mm)
d _K = Außendurchmesser Kopfauflage (mm)
d _i = Bohrungsdurchmesser (mm)
P   = Gewindesteigung (mm)
μ _G = Gewindereibwert (-)
β   = Flankenwinkel (Grad)

Wirkungsgrad

Der Wirkungsgrad einer Schraubenverbindung berechnet sich aus der Arbeit der Schraube bei einer Umdrehung, zur der Arbeit mit der die Schraube um eine Umdrehung mit dem Gabelschlüssel aufgebracht werden muss.

Wirkungsgrad beim Anziehen

Wirkungsgrad beim Lösen

η   = Wirkungsgrad (-)
φ   = Steigungswinkel (Grad)
ρ'   = Reibungswinkel Gewinde (Grad)
β   = Flankenwinkel (Grad)
μ   = Reibwert Gewinde (-)
d ₂ = Flankendurchmesser (mm)
P   = Gewindesteigung (mm)
F _v = Vorspannkraft = Axialkraft (N)
F _Hand = Handkraft (N)
l   = Länge Hebelarm (mm)

η   = Wirkungsgrad (-)
φ   = Steigungswinkel (Grad)
ρ'   = Reibungswinkel Gewinde (Grad)
β   = Flankenwinkel (Grad)
μ   = Reibwert Gewinde (-)
d ₂ = Flankendurchmesser (mm)
P   = Gewindesteigung (mm)
F _v = Vorspannkraft = Axialkraft (N)
F _Hand = Handkraft (N)
l   = Länge Hebelarm (mm)

Wegübersetzung eines Gewindes

Die Wegübersetzung ist das Verhältnis des Umfangswegs des Flankendurchmessers zur vertikalen Steigung des Gewindes, bei einer Umdrehung.

i   = Wegübersetzung (-)
d ₂ = Flankendurchmesser (mm)
P   = Gewindesteigung (mm)
φ   = Steigungswinkel (Grad)

i   = Wegübersetzung (-)
d ₂ = Flankendurchmesser (mm)
P   = Gewindesteigung (mm)
φ   = Steigungswinkel (Grad)

Pressung

Flächenpressung Kopfauflage

Die zwischen Schraubenkopf und Flansch auftretende Pressung darf die zulässige Pressung nicht überschreiten.

p _K = Flächenpressung Kopfauflage (N/mm²)
F _V =Vorspannkraft (N)
F _S,A = Axialkraftanteil auf die Schraube (N)
A _p = Pressungsfläche (mm²)
d _k = Außendurchmesser Kopfauflage (mm)
d _i = Bohrungsdurchmesser (mm) Grenzflächenpressung für Kopfauflage

p _K = Flächenpressung Kopfauflage (N/mm²)
F _V =Vorspannkraft (N)
F _S,A = Axialkraftanteil auf die Schraube (N)
A _p = Pressungsfläche (mm²)
d _k = Außendurchmesser Kopfauflage (mm)
d _i = Bohrungsdurchmesser (mm) Grenzflächenpressung für Kopfauflage

Werkstoffwerte von Schrauben und Kennzeichnung

Werkstoffwerte der Schraube für die verschiedenen Festigkeitsklassen

Werkstoffwerte der Mutter für die verschiedenen Festigkeitsklassen

Die Prüfspannung σ_ZL entspricht der größtmöglichen Zugfestigkeit einer Schraube, mit der die Mutter gepaart werden kann, wenn die Belastbarkeit der Verbindung bis zur Bruchlast der Schraube gewährleistet sein soll.

Kennzeichnung der Festigkeitsklasse von Schrauben

Nach Norm sind Schrauben ab Gewindedurchmesser M5 mit einem Herkunfts-Kennzeichen und mit dem Festigkeitsklassenkennzeichen zu versehen.
Die Kennzeichnung kann auf der Kopffläche oder Schlüsselfläche gekennzeichnet werden.

Kennzeichnung der Festigkeitsklasse von Sechskantmuttern

Die Sechskantmuttern müssen auf der Auflagefläche oder einer Schlüsselfläche vertieft oder auf der Fase erhöht gekennzeichnet werden.
Alternativ zur Kennzeichnung durch die Kennzahl der Festigkeitsklasse kann eine Kennzeichnung auch mit Hilfe des Uhrzeigersystems erfolgen.

Festigkeit	04(*	05(*	4	5	6	8	10	12
Kennzeichnung im Uhrzeigersinn

(* Schrauben und Muttern mit reduzierter Belastbarkeit (geringere Kopfhöhe) werden mit einer vorangestellten 0 gekennzeichnet.

Kennzeichnung von Linksgewinde

Schrauben mit Linksgewinde werden mit einem Pfeil auf dem Kopf oder am Gewindeende oder mit einer Einkerbung an der Schlüsselfläche markiert.

Paarung von Schrauben und Muttern [2]

Bei einer Schrauben-Mutter-Verbindung kann die Festigkeitsklasse der Mutter höher gewählt werden, als die Festigkeitsklasse der Schraube. Dies ist ratsam für eine Schrauben-Mutter-Verbindung mit Belastungen oberhalb der Streckgrenze.

¹⁾ vergüteter Werkstoff
Mutter Typ 1 = Mutterhöhe ≈ 0,9 * d - ISO 4032
Mutter Typ 2 = Mutterhöhe ≈ 1,0 * d - ISO 4033

Mindesteinschraubtiefe

Richtwerte für die Mindesteinschraubtiefe

Richtwerte für die Mindesteinschraubtiefe von Sacklochbohrungen bei verschiedenen Werkstoffpaarungen.

d = Schraubennenndurchmesser
P = Gewindesteigung

Mindesteinschraubtiefe nach VDI 2230 Febr. 2003 in Abhängigkeit der Scherfestigkeit des Innengewinde-Werkstoffs

Gültig für Regelgewinde von M4 bis M39 nach DIN 13. Toleranzklasse 6g/6H

L_eff = effektive tragende Gewindelänge

Scherfestigkeit

Nach der Gestaltänderungs-Hypothese von Mises lässt sich die Scherfestigkeit für duktile Werkstoffe wie folgt berechnen.
Welche Werkstoffkennwerte zu verwenden sind, richtet sich nach dem Nachweisziel.
Beim Nachweis der Tragfähigkeit ist die Zugfestigkeit, beim Betriebsnachweis die Streckgrenze einzusetzen.

τ = Scherfestigkeit (N/mm²)
R _m = Zugfestigkeit (N/mm²)
R _p = Streckgrenze (N/mm²)
β   = Scherspannungsfaktor (-))

τ = Scherfestigkeit (N/mm²)
R _m = Zugfestigkeit (N/mm²)
R _p = Streckgrenze (N/mm²)
β   = Scherspannungsfaktor (-))

Der Scherspannungsfaktor für die einzelnen Werkstoffe beträgt: [1]

Gewindeeinsatz Helicoil®

Mit dem Drahtgewindeeinsatz Helicoil® wird eine gleichmäßige Last- und Spannungsverteilung erzeugt.
Heliciol® Gewindeeinsätze schaffen hochfeste, verschleißfeste, thermisch belastbare Gewinde, indem die Kräfte von Flanke zu Flanke in das Aufnahmegewinde übertragen werden.

Spannung im 1. Gewindegang des Aufnahmewerkstücks

σ_w = Spannung im 1. Gewindegang des Werkstücks (N/mm²)
F _v =Vorspannkraft (N)
D _HC = Außendurchmesser Aufnahmegewinde (mm)
D _1HC = Gewindekerndurchmesser (mm)
Abmessungen siehe Hersteller Böllhoff

Mindestwandstärke

Mindestwandstärke und minimale Werkstückbreite.
Die angegebenen Richtwertformeln gelten für Aluminium-, Guss-und Knetlegierungen und eine Gewinde-Einschraublänge 1,5 d.

a_min = Mindestwandstärke (mm)
s _min = min. werkstückbreite (mm)
D _HC = Außendurchmesser Aufnahmegewinde (mm)

a_min = Mindestwandstärke (mm)
s _min = min. werkstückbreite (mm)
D _HC = Außendurchmesser Aufnahmegewinde (mm)

Erforderliche Gewindelänge (mm) von Helicoileinsätzen

Die Mindestgewindelängen sind so ausgelegt, dass Schrauben das schwächste Glied in der Verbindung sind.

Edelstahlschrauben

Allgemeines

Edelstahl wird fälschlicherweise oftmals als “nichtrostend” bezeichnet, richtiger wäre die Edelstahlsorten sind schwer rostende Edelstähle. Trotz alledem sind Edelstahlschrauben aufgrund ihrer Korrosionsbeständigkeit beliebt, sie rosten also besonders schwer.
Im Inland im Außenbereich, ohne in Berührung mit Säure zu kommen, reicht eine A2 Edelstahl Schraube vollkommen aus.
Schrauben die aus A4 Edelstahl bestehen sind zusätzlich auch noch säure- bzw – seewasserbeständig. Das bedeutet, dass gerade in Küstenregionen A4 Schrauben ihren Bestimmungsort finden. Auch in der Chemie- und Lebensmittelindustrie werden vorzugsweise A4 Edelstahl Schrauben verwendet, da diese auch Säuren standhalten.

Bezeichnung für nichtrostende Stahlsorten und die Festigkeitsklassen für Schrauben

Mechanische Eigenschaften von Edelstahlschrauben

Festigkeitswerte bei Raumtemperatur.

Änderung der Streckgrenze bei erhöhter Temperatur - Festigkeitsklasse 70 und 80

Stahlsorten und Beständigkeit

Anziehmomente für Schrauben und Muttern aus A 2/A 4

Bei Verbindungselementen aus nichtrostenden Stählen sind die Reibungswerte im Gewinde und an den Auflageflächen wesentlich größer als bei vergüteten Stahlschrauben - auch der Streubereich der Reibungswerte ist hier viel größer. Durch Verwendung von Spezialschmiermitteln können zwar die Reibungszahlen µ verringert werden - aber der sehr große Streubereich bleibt erhalten.

Reibwerte für Edelstahlschrauben

Schrauben und Muttern aus A2 oder A4