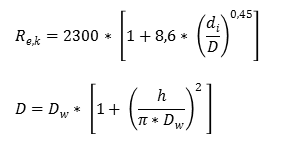Weitere Kapitel auf der Webseite zur Strömungstechnik
nach oben
Allgemeine Formeln
Strömungsgeschwindigkeit
Die Strömungsgeschwindigkeit, oder auch FlieĂgeschwindigkeit gibt die Geschwindigkeit einer Strömung an.
FĂŒr die Berechnung des Volumenstroms wird die Strömungsgeschwindigkeit und Rohrquerschnitt benötigt.
nach oben
Volumenstrom
Der Volumenstrom oder Durchflussrate und Durchflussmenge genannt, gibt an, wie viel Volumen eines Mediums
pro Zeitspanne durch einen festgelegten Querschnitt transportiert wird.
Q = Volumenstrom (mÂł/s)
V = Volumen (mÂł)
t = Zeitabschnitt (s)
v = Strömungsgeschwindigkeit (m/s)
A = Strömungsquerschnitt (mÂČ)
Q = Volumenstrom (mÂł/s)
V = Volumen (mÂł)
t = Zeitabschnitt (s)
v = Strömungsgeschwindigkeit (m/s)
A = Strömungsquerschnitt (mÂČ)
nach oben
Massenstrom
Der Massenstrom, auch Massendurchsatz, ist die Masse eines Mediums, das sich pro Zeitspanne durch einen Querschnitt bewegt.
Aus dem Volumenstrom und der Dichte kann der Massenstrom abgeleitet werden.
m = Massenstrom (kg/s)
Q = Volumenstrom (mÂł/s)
Ï = Dichte (kg/mÂł)
v = Strömungsgeschwindigkeit (m/s)
A = Strömungsquerschnitt (mÂČ)
m = Massenstrom (kg/s)
Q = Volumenstrom (mÂł/s)
Ï = Dichte (kg/mÂł)
v = Strömungsgeschwindigkeit (m/s)
A = Strömungsquerschnitt (mÂČ)
nach oben
Hydraulischer Durchmesser bei verschiedenen Querschnittsformen
Die meisten Formeln in der Strömungstechnik beziehen sich auf den Durchmesser eines runden Rohres.
Bei abweichenden Formen von einem Kreisrohr, kann mit dem hydraulischen Durchmesser davon ausgegangen werden,
dass annÀhrend die gleichen StrömungsverhÀltnisse und Druckverluste wie beim Kreisrohr herrschen.
Die Anwendung des hydraulischen Durchmessers stellt fĂŒr turbulente
Strömungen eine gute NĂ€herung dar, fĂŒr laminare StrömungsverhĂ€ltnisse kann sie jedoch zu erheblichen
Fehlern fĂŒhren.
nach oben
Dynamische ViskositÀt
Die dynamische ViskositĂ€t ist ein MaĂ fĂŒr die ZĂ€higkeit oder ZĂ€hflĂŒssigkeit eines Fluids.
η = Dynamische ViskositĂ€t (Pa*s - kg/(m*s) - N*s/mÂČ)
Îœ = Kinematische ViskositĂ€t (mÂČ/s)
Ï = Dichte (kg/mÂł)
ViskositÀtswerte siehe
Stoffwerte
η = Dynamische ViskositĂ€t (Pa*s - kg/(m*s) - N*s/mÂČ)
Îœ = Kinematische ViskositĂ€t (mÂČ/s)
Ï = Dichte (kg/mÂł)
ViskositÀtswerte siehe
Stoffwerte
nach oben
Kinematische ViskositÀt
Als kinematische ViskositÀt bezeichnet man den Quotienten aus der dynamischen ViskositÀt des Mediums und seiner Dichte.
Îœ = Kinematische ViskositĂ€t (mÂČ/s)
η = Dynamische ViskositÀt (Pa*s)
Ï = Dichte (kg/mÂł)
ViskositÀtswerte siehe
Stoffwerte
Îœ = Kinematische ViskositĂ€t (mÂČ/s)
η = Dynamische ViskositÀt (Pa*s)
Ï = Dichte (kg/mÂł)
ViskositÀtswerte siehe
Stoffwerte
nach oben
Reynoldszahl
Die Reynoldszahl wird in der Strömungslehre dazu verwendet die Strömungsart zu bestimmen. In der Strömungslehre existieren zwei
verschiedene Strömungsarten, die bei Fluiden (FlĂŒssigkeiten oder Gasen) auftreten können:
Die laminare Strömung ohne Verwirbelungen und die turbulente Strömung mit Verwirbelungen.
R
e = Reynolds-Zahl (-)
v = Strömungsgeschwindigkeit (m/s)
Ï = Dichte (kg/mÂł)

= kinematische ViskositĂ€t (mÂČ/s)
d
H = hydraulischer Durchmesser (m) - bzw. charakteristische LĂ€nge
η = dynamische ViskositÀt (Pa s)
m = Massenstrom (kg/s)
R
e = Reynolds-Zahl (-)
v = Strömungsgeschwindigkeit (m/s)
Ï = Dichte (kg/mÂł)

= kinematische ViskositĂ€t (mÂČ/s)
d
H = hydraulischer Durchmesser (m) - bzw. charakteristische LĂ€nge
η = dynamische ViskositÀt (Pa s)
m = Massenstrom (kg/s)
nach oben
Kritische Reynoldszahl
Bei der kritischen Reynolds-Zahl, findet der Ăbergang von laminarer zu turbulenter Strömung statt.
FĂŒr ein rundes glattes Rohr ist die kritische Reynoldszahl 2320.
- Laminare Strömung Re < 2320
- Turbulente Strömung Re > 2320
Die kritische Reynoldszahl ist von der Strömungsgeometrie abhÀngig, in der Praxis ist man auf empirische Messungen angewiesen, die
laminare und turbulente Bereiche beschreiben.
FĂŒr folgende Strömungsgometrien gelten nach [1] folgende kritische Reynoldszahlen:
- Kugel Re,krit = 170000 ... 400000
- Platte Re,krit = 320000 ... 1000000
nach oben
Kritische Reynoldszahl in einer Rohrwendel
In Rohrschlangen verschiebt sich gegenĂŒber dem geraden Rohr der Umschlag von laminarer zu turbulenter Strömung mit zunehmendem
KrĂŒmmungsverhĂ€ltnis d/D zu höheren kritischen Reynoldszahlen.
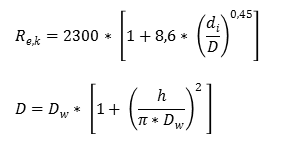
Merkliche Unterschiede zwischen D und Dw ergeben sich nur fĂŒr
stark gekrĂŒmmte Rohre mit groĂer Steigung h der Wendel.
 Zetawert fĂŒr Rohrwendel
Zetawert fĂŒr Rohrwendel
R e,k = kritische Reynolds-Zahl (-)
d i = Rohrinnendurchmesser (mm)
D w = Durchmesser der Wendel (mm)
h = Steigung der Wendel (mm)
R e,k = kritische Reynolds-Zahl (-)
d i = Rohrinnendurchmesser (mm)
D w = Durchmesser der Wendel (mm)
h = Steigung der Wendel (mm)
nach oben
KontinuitÀtsgleichung
Die KontinuitĂ€tsgleichung fĂŒr den Volumenstrom besagt, dass ein Volumenstrom (Strömung) in einer Leitung immer konstant ist.
Dies Àndert sich auch nicht, wenn sich der Querschnitt der Leitung verÀndert. Einfach gesagt, was vorne reinkommt, muss auch hintern wieder herauskommen.
m = Massenstrom (kg/s)
v = Strömungsgeschwindigkeit (m/s)
A = Strömungsquerschnitt (mÂČ)
Ï = Dichte (kg/mÂł)
d = Rohrinnendurchmesser (m)
m = Massenstrom (kg/s)
v = Strömungsgeschwindigkeit (m/s)
A = Strömungsquerschnitt (mÂČ)
Ï = Dichte (kg/mÂł)
d = Rohrinnendurchmesser (m)
nach oben
Bernoulligleichung
Die Gesamtenergie eines Teilchens auf seinem Weg in einer Stromröhre bleibt konstant, bei reibungsfreier Strömung und keiner zu- oder
abfĂŒhren Energie.
Die Bernoulligleichung sowie die erweiterte Bernoulligleichung mir reibungsbehafteter Strömung und Energiezufuhr (Pumpe),
sind in dem folgenden Link aufgefĂŒhrten.
nach oben
Druckverlust inkompressibler Medien (FlĂŒssigkeiten)
Druckverlust durch Rohrreibung
Durch die Strömung eines Fluides durch ein Rohr, entsteht ein Druckverlust durch Reibung.
Die Reibung entsteht an den InnenwÀnden des Rohres.
Der Druckverlust im geraden Rohr, wird durch die Rohrreibungszahl λ ermittelt.
Sie hÀngt bei einer laminaren Strömung von der Reynoldszahl ab, und bei einer turbulenten Strömung dagegen geht insbesondere die Rauheit der OberflÀche mit ein.
Î p = Druckverlust durch Rohrreibung (Pa)
λ = Rohrreibungszahl (-)
L = RohrlÀnge (m)
Ï = Dichte (kg/mÂł)
v = Strömungsgeschwindigkeit (m/s)
d i = Rohrinnendurchmesser (m)
Î p = Druckverlust durch Rohrreibung (Pa)
λ = Rohrreibungszahl (-)
L = RohrlÀnge (m)
Ï = Dichte (kg/mÂł)
v = Strömungsgeschwindigkeit (m/s)
d i = Rohrinnendurchmesser (m)
nach oben
Berechnungsprogramm: Druckverlustberechnung gerade Rohrleitung

Berechnung des Druckverlust einer kreisförmigen geraden Rohrleitung.
Es können verschiedene Medien ausgewÀhlt werden. Wird ein Medium ausgewÀhlt, wird die Dichte und ViskositÀt in AbhÀngigkeit von der
Temperatur vom Programm ermittelt.
Bei Selektion von "Eingabewerte" ist die Dichte und ViskositÀt selbst einzugeben.
nach oben
Berechnungsprogramm: Druckverlustberechnung Rohrleitungsstrang
Druckverlustberechnung eines Rohrleitungsstrangs mit verschiedenen Komponenten wie:
 Rohrleitung, RohrkrĂŒmmer, konische und plötzliche Rohraufweitung und -verengung.
Rohrleitung, RohrkrĂŒmmer, konische und plötzliche Rohraufweitung und -verengung.
Bei Eingabe einer Pumpenkennlinie, wird in einem Diagramm mit Anlagen- und Pumpenkennlinie der tatsÀchliche Betriebspunkt
dargestellt.
nach oben
Druckverlust durch geodÀtische Höhendifferenz
Die Berechnung des geodÀtischen Druckes ist aus der Bernoulli Gleichung abgeleitet und beschreibt den Druck am unteren Ende der FluidsÀule,
der durch das Eigengewicht des Fluides entsteht.
Der Höhenunterschied zwischen der Pumpe und der Entnahmestelle wird als geodÀtische Höhe bezeichnet.
ÎpH = Druckverlust durch Höhendifferenz (Pa)
Ï Luft = Dichte Umgebungsluft (kg/m3)
Ï F = Dichte FlĂŒssigkeit (kg/m3)
H 1 = geodĂ€tische Starthöhe in FlieĂrichtung (m)
H 2 = geodĂ€tische Zielhöhe in FlieĂrichtung (m)
g = Fallbeschleunigung (m/s2)
ÎpH = Druckverlust durch Höhendifferenz (Pa)
Ï Luft = Dichte Umgebungsluft (kg/m3)
Ï F = Dichte FlĂŒssigkeit (kg/m3)
H 1 = geodĂ€tische Starthöhe in FlieĂrichtung (m)
H 2 = geodĂ€tische Zielhöhe in FlieĂrichtung (m)
g = Fallbeschleunigung (m/s2)
nach oben
Druckverlust durch Armaturen, FormstĂŒcke usw.
Bei Durchströmung der verschiedenen Armaturen und FormstĂŒcke treten je nach Geometrie und
Ăffnungszustand unterschiedliche Druckverluste auf.
Infolge der oft starken Umlenkung der Strömung innerhalb der Armatur, treten im voll geöffneten Zustand auch Druckverluste auf.
Der Druckverlust wird fĂŒr die verschiedenen Armaturen durch den Zetawert ζ ausgedrĂŒckt, der experimentell ermittelt wird.
Î p
ζ = Druckverlust durch Armaturen (Pa)
ζ = Zetawert (-) siehe Kapitel
Zetawerte
Ï = Dichte (kg/mÂł)
v = Strömungsgeschwindigkeit (m/s)
V
= Volumenstrom (m
3/s)
A
= Rohrleitungsquerschnitt (m
2)
Î p
ζ = Druckverlust durch Armaturen (Pa)
ζ = Zetawert (-) siehe Kapitel
Zetawerte
Ï = Dichte (kg/mÂł)
v = Strömungsgeschwindigkeit (m/s)
V
= Volumenstrom (m
3/s)
A
= Rohrleitungsquerschnitt (m
2)
nach oben
Druckverlust in einer Rohrwendel
Bei der Strömung eines Fluides durch eine Rohrwendel, treten durch die KrĂŒmmung des Rohres ZentrifugalkrĂ€fte auf,
die eine SekundÀrströmung in Form eines Doppelwirbels hervorrufen.
Die SekundÀrströmung bewirkt eine Erhöhung des Druckverlusts.
Î p
ζ = Druckverlust in der Rohrwendel (Pa)
ζ =
Zetawert Rohrwendel (-)
l
= LĂ€nge der gesamten Rohrwendel (m)
Ï = Dichte (kg/mÂł)
v = Strömungsgeschwindigkeit (m/s)
d
i = Rohrinnendurchmesser (m)
Î p
ζ = Druckverlust in der Rohrwendel (Pa)
ζ =
Zetawerte Rohrwendel (-)
l
= LĂ€nge der gesamten Rohrwendel (m)
Ï = Dichte (kg/mÂł)
v = Strömungsgeschwindigkeit (m/s)
d
i = Rohrinnendurchmesser (m)
nach oben
Ăquivalente RohrlĂ€nge fĂŒr Armaturen FormstĂŒcke usw.
FĂŒr ĂŒberschlĂ€gige Druckverlustberechnungen, wird fĂŒr Armaturen manchmal eine Ă€quivalente RohrlĂ€nge zur der RohrlĂ€nge des geraden Rohrs
dazu addiert.
Die Àquivalente RohrlÀnge wird nach folgender Formel berechnet:
Là = Àquivalente RohrlÀnge (m)
ζ = Zetawert (-)
d i = Rohrinnendurchmesser (m)
λ = Rohrreibungszahl des geraden Rohres (-)
Là = Àquivalente RohrlÀnge (m)
ζ = Zetawert (-)
d i = Rohrinnendurchmesser (m)
λ = Rohrreibungszahl des geraden Rohres (-)
nach oben
Druckverlust aus der Druckverlustangabe bei maximalem Volumenstrom
FĂŒr Apparate werden von Herstellern oftmals keine Einzelwiderstandszahlen ζ angegeben, sondern der maximale Druckverlust im VerhĂ€ltnis
zum max. Volumenstrom.
Der tatsÀchliche Druckverlust berechnet sich wie folgt:
Îptat = tatsĂ€chlicher Druckverlust (Pa)
Îp max = max. Druckverlust bei max. Volumenstrom (Pa)
V tat = tatsÀchlicher Volumenstrom (m3/h)
V max = max. Volumenstrom (m3/h)
Îptat = tatsĂ€chlicher Druckverlust (Pa)
Îp max = max. Druckverlust bei max. Volumenstrom (Pa)
V tat = tatsÀchlicher Volumenstrom (m3/h)
V max = max. Volumenstrom (m3/h)
nach oben
Druckverlust Kreisringquerschnitt
FĂŒr die Berechnung des Druckverlustes eines Rohrquerschnittes sind folgende Daten zu ermitteln:
- Strömungsgeschwindigkeit berechnet aus dem Volumenstrom und der QuerschnittsflÀche
- Hydraulischer Durchmesser berechnen ( bei Kreisrohr dh = d)
- Aus der Strömungsgeschwindigkeit, dem hydraulischen Durchmesser und der kinematischen ViskositÀt des Mediums, berechnet man die Reynoldszahl
- Die dimensionslose Rohrreibungszahl kann berechnet
oder aus Diagrammen in AbhÀngigkeit der Àquivalenten Rohrrauigkeit und der Reynoldszahl ermittelt werden
- Der Druckverlust des Rohrs wird dann mit o. g. Daten und der RohrlÀnge berechnet.
Berechnung Strömungsgeschwindigkeit Kreisring

Hydraulischer Durchmesser Kreisring

Berechnung Reynoldszahl

Bei der Bestimmung der Rohrreibungszahl, ist die equivalente Rauhigkeit

Druckverlust Kreisring

v = Strömungsgeschwindigkeit (m/s)
Q = Volumenstrom (mÂł/s)
d
a = RohrauĂendurchmesser (m)
d
i = Rohrinnendurchmesser (m)
d
h = Hydraulischer Rohrdurchmesser (m)
R
e = Reynolds-Zahl (-)

= kinematische ViskositĂ€t (mÂČ/s)
k = Rohrrauigkeit (m)
Îp = Druckverlust (Pa)
λ = Rohrreibungszahl (-)
L = RohrlÀnge (m)
Ï = Dichte (kg/mÂł)

v = Strömungsgeschwindigkeit (m/s)
Q = Volumenstrom (mÂł/s)
d
a = RohrauĂendurchmesser (m)
d
i = Rohrinnendurchmesser (m)
d
h = Hydraulischer Rohrdurchmesser (m)
R
e = Reynolds-Zahl (-)

= kinematische ViskositĂ€t (mÂČ/s)
k = Rohrrauigkeit (m)
Îp = Druckverlust (Pa)
λ = Rohrreibungszahl (-)
L = RohrlÀnge (m)
Ï = Dichte (kg/mÂł)

nach oben
Druckverlust laminare Strömung - Hagen-Poiseuille Gesetz
Das Hagen-Poiseuillesches Gesetz, beschreibt die laminare Strömung einer inkompressiblen viskosen FlĂŒssigkeit in einem Röhrchen von
kreisförmigem Querschnitt. Das Gesetz gilt nur fĂŒr laminare Strömungen. Bei gröĂerem Durchfluss einer Rohrleitung, verbunden mit höheren
Strömungsgeschwindigkeiten bzw. gröĂeren Abmessungen, kommt es zu turbulenten Strömungen mit wesentlich höherem
Strömungswiderstand.
V = Volumenstrom (mÂł/s)
r = Innenradius Rohr (m)
Îp = Druckverlust (Pa)
η = Dynamische ViskositÀt (Pa*s)
l = RohrlÀnge (m)
b = Breite (m)
h = Höhe (m)
K = Konstante (-)
a = minimaler Durchmesser (m)
b = maximaler Durchmesser (m)
V = Volumenstrom (mÂł/s)
r = Innenradius Rohr (m)
Îp = Druckverlust (Pa)
η = Dynamische ViskositÀt (Pa*s)
l = RohrlÀnge (m)
b = Breite (m)
h = Höhe (m)
K = Konstante (-)
a = minimaler Durchmesser (m)
b = maximaler Durchmesser (m)
nach oben
DruckstoĂ (Joukowsky)
Ein Druckstoà wird durch in stationÀre Strömungen hervorgerufen, die bei allen RegelvorgÀngen in Rohrleitungen, mehr oder minder stark,
auftreten. In stationÀre Bedingungen treten immer dann auf, wenn sich die Strömungsgeschwindigkeit mit der Zeit verÀndert, z. B. beim
schnellen SchlieĂen einer Absperrarmatur.
Differenzdruck

Wellenfortpflanzungsgeschwindigkeit

Îp = DruckĂ€nderung (N/m2)
Ï = Dichte Medium (kg/m3)
a = Wellenfortpflanzungsgeschwindigkeit (m/s)
Îv = GeschwindigkeitsĂ€nderung (m/s)
E F = Kompressionsmodul des Mediums (N/m2)
E R = E-Modul der Rohrwand (N/m2)
d = Rohrinnendurchmesser (m)
s = Rohrwanddicke (m)
Îp = DruckĂ€nderung (N/m2)
Ï = Dichte Medium (kg/m3)
a = Wellenfortpflanzungsgeschwindigkeit (m/s)
Îv = GeschwindigkeitsĂ€nderung (m/s)
E F = Kompressionsmodul des Mediums (N/m2)
E R = E-Modul der Rohrwand (N/m2)
d = Rohrinnendurchmesser (m)
s = Rohrwanddicke (m)
nach oben
Die o. g. Formel ist nur eine NĂ€herungsformel, da der Gasgehalt in der FlĂŒssigkeit unberĂŒcksichtigt ist. Dieser kann die
Wellenfortpflanzungsgeschwindigkeit nÀmlich stark verÀndern (Tabelle Wasser bei 3 bar Wasserdruck).
| Gasgehalt (Vol %) |
Wellenfortpflanzungs-
geschwindigkeit - a (m/s) |
| 0 |
1250 |
| 0,2 |
450 |
| 0,4 |
300 |
| 0,8 |
250 |
| 1,0 |
240 |
nach oben
DruckstoĂ in Rohrleitungen unter Beachtung der SchlieĂzeit
Die SchlieĂzeit eines Regelorganes hat entscheidenden Einfluss auf die Höhe des DruckstoĂes und wird erst relevant, wenn sie oberhalb der Reflexionszeit liegt.
Dann nĂ€mlich trifft die Welle nach Reflexion, noch vor dem vollstĂ€ndigen SchlieĂen des Reglers dort ein und kann sich so teilweise entspannen.
Unterhalb der Reflexionszeit tritt immer der volle Joukowsky-StoĂ auf.
Reflexionszeit

DruckÀnderung

TR = Reflexionszeit (s)
T S = SchlieĂzeit der Armatur (s)
L = RohrleitungslÀnge (m)
a = Wellenfortpflanzungsgeschwindigkeit (m/s)
Îp = DruckĂ€nderung (N/m2)
Ï = Dichte Medium (kg/m3)
Îv = GeschwindigkeitsĂ€nderung (m/s)
TR = Reflexionszeit (s)
T S = SchlieĂzeit der Armatur (s)
L = RohrleitungslÀnge (m)
a = Wellenfortpflanzungsgeschwindigkeit (m/s)
Îp = DruckĂ€nderung (N/m2)
Ï = Dichte Medium (kg/m3)
Îv = GeschwindigkeitsĂ€nderung (m/s)
nach oben
Druckverlust kompressibler Medien (Gase)
Bei Strömung von Luft, Gasen und DÀmpfen in Rohrleitungen liegt eine Expansionsströmung vor, da der Druck infolge des
Reibungsverlustes in Strömungsrichtung abnimmt.
Allgemein Àndert sich dabei lÀngs der Rohrleitung Druck, Temperatur, Dichte und Geschwindigkeit.
Der Druckabfall ist lÀngs der Rohrleitung nicht linear und die Geschwindigkeit nicht konstant.
Druckverlust bei isothermer Strömung - ohne Isolierung
Bei nicht isolierten Rohrleitungen findet ein WÀrmeaustausch statt, die Temperatur gleicht sich allmÀhlich der Umgebungstemperatur
an.
Die Strömung wird als Isotherme Strömung bezeichnet.
Mit den unten aufgefĂŒhrten Annahmen fĂŒr die Rohrreibungszahl und Temperatur kann der Druckabfall mit folgender Gleichung fĂŒr technische
Anwendungen ausreichend genau berechnet werden.
p 1 = Druck Rohranfang (Pa_abs)
Îp = Druckdifferenz (Pa)
λ = Rohrreibungszahl (-)
l = RohrlÀnge (m)
d = Rohrinnendurchmesser (m)
Ï 1 = Dichte Rohranfang (kg/mÂł)
Îœ 1 = Strömungsgeschwindigkeit Rohranfang (m/s)
p 1 = Druck Rohranfang (Pa_abs)
Îp = Druckdifferenz (Pa)
λ = Rohrreibungszahl (-)
l = RohrlÀnge (m)
d = Rohrinnendurchmesser (m)
Ï 1 = Dichte Rohranfang (kg/mÂł)
Îœ 1 = Strömungsgeschwindigkeit Rohranfang (m/s)
nach oben
Druckverlustberechnung einer kreisförmigen Rohrleitung mit trockener Luft, bei reibungsbehafteter adiabatischer Strömung.
Bei isolierten Rohrleitungen erfolgt kaum ein WĂ€rmeaustausch nach auĂen statt. Die Strömung wird als adiabate Rohrströmung
bezeichnet.
Die unten aufgefĂŒhrten Formeln gelten unter folgenden Annahmen:
- Rohrreibungszahl λ ist konstant
- QuerschnittsflÀche A ist konstant
- Isotropenkoeffizient ist konstant - Îș = 1,402 trockene Luft
v1 = Strömungsgeschwindigkeit Rohranfang (m/s)
v 2 = Strömungsgeschwindigkeit Rohrende (m/s)
λ = Rohrreibungszahl (-)
l = RohrlÀnge (m)
d = Rohrinnendurchmesser (m)
Îș = Isentropenkoeffizient (-)
M 1 = Machzahl Rohranfang (-)
a = Schallgeschwindigkeit (m/s)
T 1 = Temperatur Rohranfang (K)
T 2 = Temperatur Rohrende (K)
Ï 1 = Dichte Rohranfang (kg/mÂł)
Ï 2 = Dichte Rohrende (kg/mÂł)
p 1 = Druck Rohranfang (Pa_abs)
p 2 = Druck Rohrende (Pa_abs)
Îp = Druckdifferenz (Pa)
v1 = Strömungsgeschwindigkeit Rohranfang (m/s)
v 2 = Strömungsgeschwindigkeit Rohrende (m/s)
λ =Rohrreibungszahl (-)
l = RohrlÀnge (m)
d = Rohrinnendurchmesser (m)
Îș = Isentropenkoeffizient (-) M 1 = MAchzahl Rohranfang (-)
a = Schallgeschwindigkeit (m/s)
T 1 = Temperatur Rohranfang (K)
T 2 = Temperatur Rohrende (K)
Ï 1 = Dichte Rohranfang (kg/mÂł)
Ï 2 = Dichte Rohrende (kg/mÂł)
p 1 = Druck Rohranfang (Pa_abs)
p 2 = Druck Rohrende (Pa_abs)
Îp = Druckdifferenz (Pa)
nach oben
nach oben
Druckverlust durch Armaturen, FormstĂŒcke usw. bei kompressiblen Medien
Bei kompressiblen Medien ist fĂŒr die Druckverlustberechnung jeweils die Dichte und Strömungsgeschwindigkeit fĂŒr die einzelnen
Komponenten neu zu bestimmen. Die Dichte ist vom absoluten Druck und der Temperatur des Mediums abhÀngig. Mit abnehmendem Druck und
Temperatur nimmt die Dichte zu und somit auch das Volumen, wodurch sich die Strömungsgeschwindigkeit erhöht. Bei langen Rohrleitungen ist
dies besonders zu berĂŒcksichtigen.
Πp ζ = Druckverlust durch Armaturen (Pa)
ζ = Zetawert (-) siehe Kapitel Zetawerte
Ï = Dichte (kg/mÂł)
v = Strömungsgeschwindigkeit (m/s)
Πp ζ = Druckverlust durch Armaturen (Pa)
ζ = Zetawert (-) siehe Kapitel Zetawerte
Ï = Dichte (kg/mÂł)
v = Strömungsgeschwindigkeit (m/s)
nach oben
Rohrreibungszahl
Die Rohrreibungszahl λ ist eine Funktion der Reynoldszahl Re und der relativen Wandrauigkeit d/k.
Man unterscheidet folgende typische Rauigkeitsbereiche:
- Hydraulisch glatte OberflÀche
- Hydraulisch raue OberflÀche
- Ăbergangsbereich zwischen rauer und glatter OberflĂ€che.
nach oben
Hydraulisch glatte OberflÀche
Formel nach Prandtl und K'arm'an - Grenzbereich Re > 2300
λ = Rohrreibungszahl (-)
R e = Reynolds-Zahl (-)
iterativ berechnen
λ = Rohrreibungszahl (-)
R e = Reynolds-Zahl (-)
iterativ berechnen

nach oben
Hydraulisch raue OberflÀche
Formel nach Nikuradse - Grenzbereich Re = 200 * d / (λ 0,5 * k)
λ = Rohrreibungszahl (-)
d = Rohrinnendurchmesser (m)
k = Rohrrauigkeit (m)
λ = Rohrreibungszahl (-)
d = Rohrinnendurchmesser (m)
k = Rohrrauigkeit (m)

nach oben
Ăbergangsbereich von rauer zur glatten OberflĂ€che
Formel nach Prandtl und Colebrook - Grenzbereich Re = 200 * d / (λ 0,5 * k)
λ = Rohrreibungszahl (-)
R e = Reynolds-Zahl (-)
d = Rohrinnendurchmesser (m)
k = Rohrrauigkeit (m)
iterativ berechnen
λ = Rohrreibungszahl (-)
R e = Reynolds-Zahl (-)
d = Rohrinnendurchmesser (m)
k = Rohrrauigkeit (m)
iterativ berechnen

nach oben
Grenzwert fĂŒr raue OberflĂ€che
λ = Rohrreibungszahl (-)
R e = Reynolds-Zahl (-)
d = Rohrinnendurchmesser (m)
k = Rohrrauigkeit (m)
λ = Rohrreibungszahl (-)
R e = Reynolds-Zahl (-)
d = Rohrinnendurchmesser (m)
k = Rohrrauigkeit (m)

nach oben
Diagramm - Rohrreibungszahl in AbhÀngigkeit von Re und d/k
Diagramm der Rohrreibungszahl in AbhÀngigkeit der Reynoldszahl und der Àquivalenten Rauigkeit
(d/k).

nach oben
NĂ€herungsformel fĂŒr die Rohrreibungszahl im Ăbergangsbereich
FĂŒr Ăberschlagsberechnungen kann die folgende Formel fĂŒr die Rohrreibungszahl verwendet werden. Die Rohrreibungszahl befindet sich im
Ăbergangsbereich, d. h. Rohre mit geringer Rohrrauigkeit.
λ = Rohrreibungszahl (-)
Re = Reynoldszahl (-)
λ = Rohrreibungszahl (-)
Re = Reynoldszahl (-)

nach oben
Laminare Strömung
Laminare Strömung tritt bei Re < 2300 auf.
Die Rohrreibungszahl hÀngt von der Geometrie des Querschnitts ab. Die Querschnittsform wird durch den
Korrekturfaktor C berĂŒcksichtigt.

C = 64 - Kreisquerschnitt
C = 53 - gleichschenkliges-rechtwinkliges Dreieck
C = 57 - gleichseitiges Dreieck
λ = Rohrreibungszahl (-)
C = Korrekturfaktor fĂŒr Querschnittsform (-)
R e = Reynolds-Zahl (-)
λ = Rohrreibungszahl (-)
C = Korrekturfaktor fĂŒr Querschnittsform (-)
R e = Reynolds-Zahl (-)

nach oben
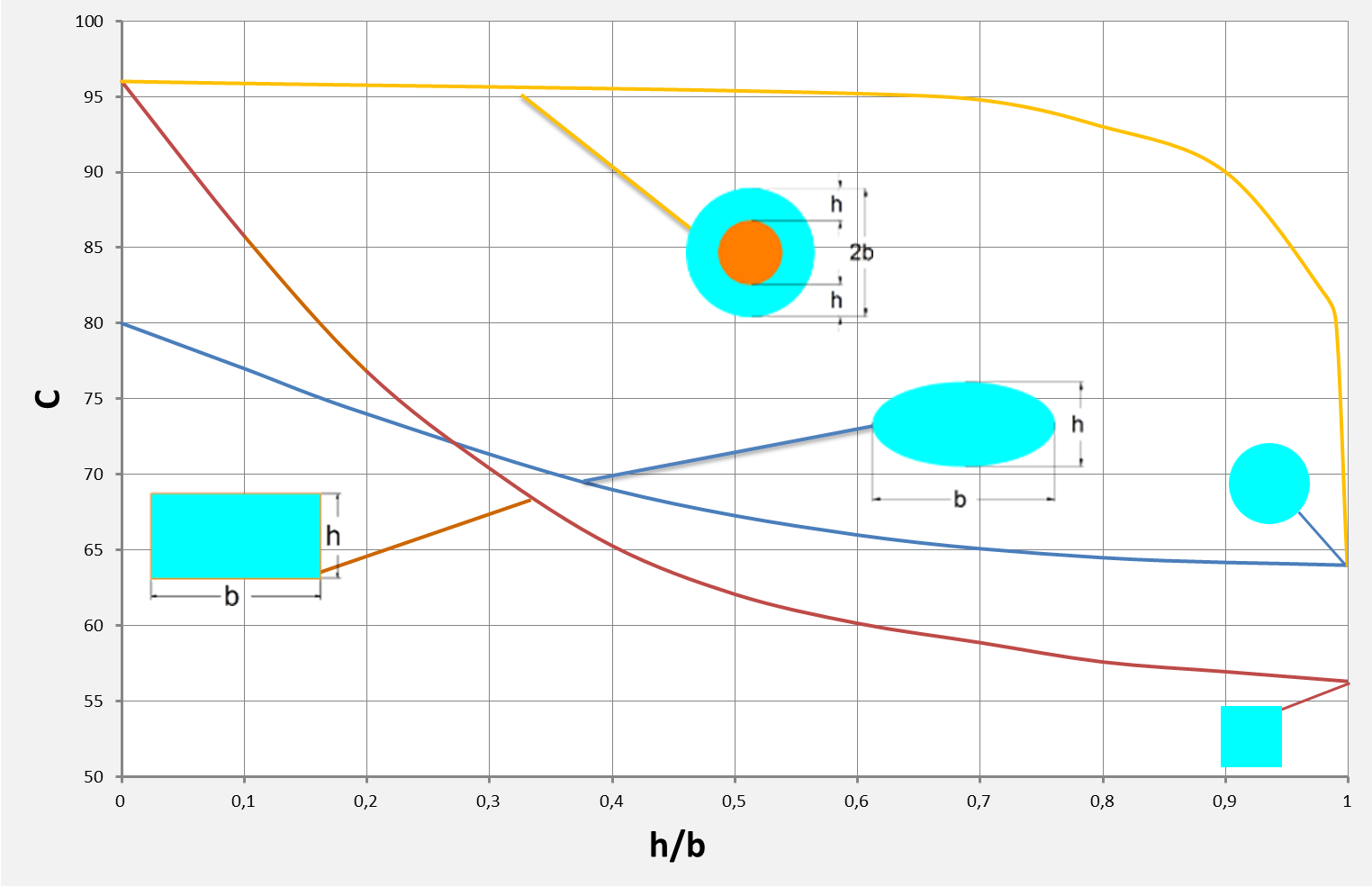
Korrekturfaktor bei laminarer Strömung [2]
Der Korrekturfaktor ist AbhÀngig von der Querschnittsform Höhe zu Breite.
Der allgemein bekannte Faktor 63 ist gĂŒltig fĂŒr einen Kreisquerschnitt (siehe Diagramm).
nach oben
Rohrreibungszahl Wellrohr [3]
FĂŒr ein Wellrohr kann die folgende NĂ€herungsformel fĂŒr die Rohrreibungszahl verwendet werden.
Die Formel ist gĂŒltig fĂŒr den turbulenten Bereich (Re â„ 50000).
Der Druckverlust ist nach der Formel fĂŒr das gerade Rohr, mit der hier ermittelten Rohrreibungszahl zu berechnen.
λ = Rohrreibungszahl (-)
d = Innendurchmesser (mm)
l = Wellenabstand (mm)
h = Wellenhöhe (mm)
b = Wellenbreite (mm)
k = Rauigkeit (mm)
λ = Rohrreibungszahl (-)
d = Innendurchmesser (mm)
l = Wellenabstand (mm)
h = Wellenhöhe (mm)
b = Wellenbreite (mm)
k = Rauigkeit (mm)
nach oben
Anlagenkennlinie - Pumpenkennlinie - Betriebspunkt
Anlagenkennlinie
Die Anlagenkennlinie ist die Kurve, die den Zusammenhang zwischen der Förderhöhe der Anlage und dem Förderstrom
wiedergibt. Das VerhÀltnis Druckverlust zu Volumenstrom im Quadrat wird auch Anlagenkennlinie bezeichnet.
p 1 = Druckverlust bei Betriebspunkt 1 (bar)
p 2 = Druckverlust bei Betriebspunkt 2 (bar)
V 1 = Volumenstrom bei Betriebspunkt 1 (mÂł/h)
V 2 = Volumenstrom bei Betriebspunkt 2 (mÂł/h)
p 1 = Druckverlust bei Betriebspunkt 1 (bar)
p 2 = Druckverlust bei Betriebspunkt 2 (bar)
V 1 = Volumenstrom bei Betriebspunkt 1 (mÂł/h)
V 2 = Volumenstrom bei Betriebspunkt 2 (mÂł/h)
nach oben
Pumpenkennlinie
Die Pumpenkennlinie wird vom Hersteller ermittelt. In AbhÀngigkeit des Volumenstroms wird die Förderhöhe der Pumpe
dargestellt.
Betriebspunkt
Der Betriebspunkt einer Pumpe stellt sich dort ein, wo die Förderhöhen der Pumpe und Anlage gleich groà sind, also dort, wo sich die
Pumpenkennlinie und die Anlagenkennlinie schneiden. Im Regelfall ist fĂŒr die Auswahl der Pumpe in einer Anlage primĂ€r der Förderstrom
maĂgebend; die Förderhöhe der Anlage wird dann entsprechend den vorgegebenen VerhĂ€ltnissen ausgelegt.

Literatur:
[1] Hering/Martin/Stohrer: Physikalisch-Technisches Taschenbuch
[2] Ritschel: Raumklimatechnik - 1. Grundlagen
[3] Bohl: Technische Strömungslehre
nach oben




































 = kinematische ViskositĂ€t (mÂČ/s)
= kinematische ViskositĂ€t (mÂČ/s)